What Is 4 Divided By 1/2
listenit
May 24, 2025 · 5 min read
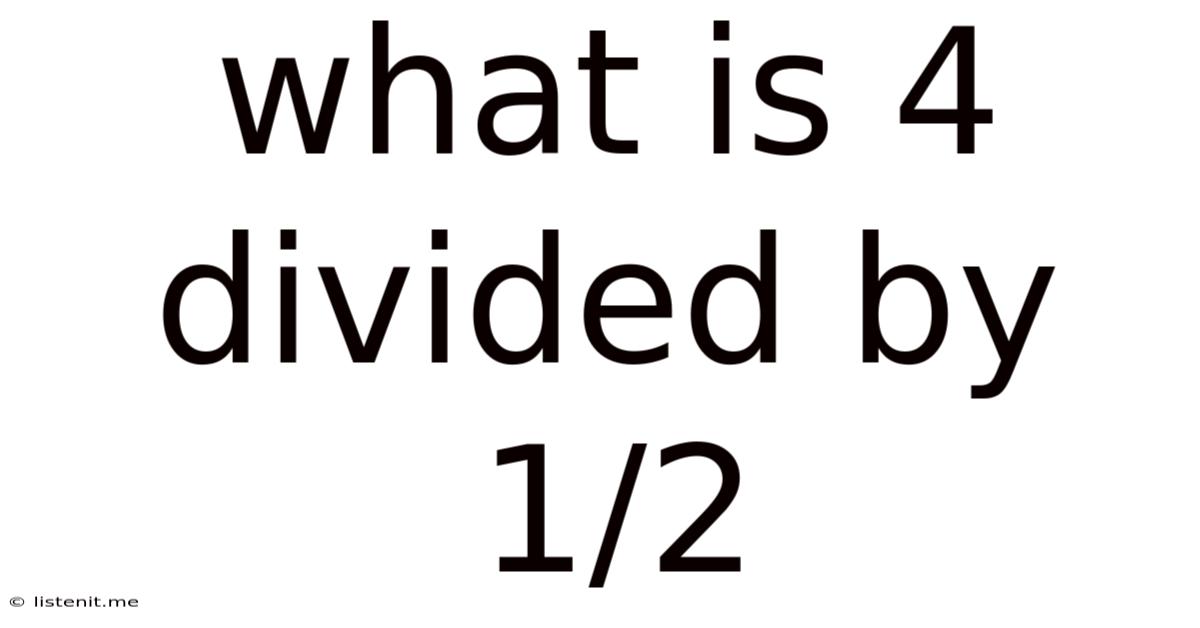
Table of Contents
What is 4 Divided by 1/2? Unpacking the Math and its Implications
The seemingly simple question, "What is 4 divided by 1/2?", often trips up students and even adults. While the answer itself is straightforward, understanding the underlying concepts reveals a deeper appreciation of fractions and division. This article will not only answer the question but also explore the mathematical principles involved, providing various approaches to solve similar problems and illustrating its relevance in real-world scenarios.
Understanding Division: The Core Concept
Before diving into the specifics of 4 divided by 1/2, let's solidify our understanding of division. Division is essentially the process of splitting a quantity into equal parts. For instance, 12 ÷ 3 means splitting 12 into 3 equal groups, resulting in 4 in each group. This can be visually represented with objects, making the concept more intuitive.
Division as Repeated Subtraction
Division can also be viewed as repeated subtraction. How many times can you subtract 3 from 12 before reaching zero? The answer, 4, is the same result obtained through standard division. This perspective proves particularly helpful when dealing with fractions, as we'll see later.
The Reciprocal: A Key Player in Fraction Division
When dividing by a fraction, a crucial concept is the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/2 is 2/1, or simply 2. This reciprocal plays a vital role in simplifying fraction division.
Solving 4 Divided by 1/2: Different Approaches
Now, let's tackle the central question: What is 4 divided by 1/2? We will explore multiple methods to solve this, enhancing comprehension and offering flexibility.
Method 1: The "Keep, Change, Flip" Method
This popular method is a shortcut for dividing fractions. It involves:
- Keeping the first number (4) as it is.
- Changing the division sign to a multiplication sign.
- Flipping (finding the reciprocal of) the second number (1/2) to become 2/1 or 2.
Therefore, 4 ÷ 1/2 becomes 4 × 2 = 8.
Method 2: Visual Representation
Imagine you have 4 pizzas. If you divide each pizza into halves (1/2), how many half-pizzas do you have? You'll have 2 half-pizzas per pizza, and with 4 pizzas, you'll have a total of 4 x 2 = 8 half-pizzas. This visual approach makes the concept tangible and easier to grasp.
Method 3: Repeated Subtraction
How many times can you subtract 1/2 from 4? You can subtract 1/2 eight times before reaching zero:
4 - 1/2 - 1/2 - 1/2 - 1/2 - 1/2 - 1/2 - 1/2 - 1/2 = 0
This reinforces the concept of division as repeated subtraction.
Method 4: Converting to Improper Fractions
Convert 4 to an improper fraction (8/2) to maintain consistency in format. Now the problem becomes: (8/2) ÷ (1/2). Applying the "keep, change, flip" method, we get (8/2) x (2/1) = 16/2 = 8. This method demonstrates the flexibility of working with fractions.
Beyond the Simple Answer: Real-World Applications
The seemingly simple calculation of 4 divided by 1/2 has significant practical applications in various real-world contexts:
-
Cooking and Baking: Recipes often require dividing ingredients. If a recipe calls for 1/2 cup of flour per serving, and you need to make 4 servings, you’ll need 4 ÷ (1/2) = 8 cups of flour.
-
Construction and Measurement: Dividing lengths or materials is a frequent task. If a piece of wood is 4 meters long, and you need pieces that are 1/2 meter each, you can make 8 pieces.
-
Data Analysis and Statistics: Understanding fraction division is fundamental to interpreting data and performing calculations involving proportions and ratios.
-
Sewing and Crafting: Cutting fabric or other materials often involves dividing lengths into specific fractions.
Expanding the Concept: Dividing by Other Fractions
The principles discussed above apply equally to dividing any number by a fraction. Let's explore a few more examples:
-
6 ÷ 1/3: Using the "keep, change, flip" method, this becomes 6 × 3 = 18.
-
10 ÷ 2/5: This becomes 10 × 5/2 = 50/2 = 25.
-
2/3 ÷ 1/4: This becomes (2/3) × (4/1) = 8/3
These examples demonstrate the broad applicability of the "keep, change, flip" method and the importance of understanding reciprocals.
Common Mistakes to Avoid
When dividing by fractions, several common mistakes can arise:
-
Forgetting to flip the second fraction: This is perhaps the most frequent error. Remember, you must find the reciprocal of the divisor (the number you're dividing by) before multiplying.
-
Incorrect multiplication of fractions: Make sure to multiply numerators and denominators correctly when applying the "keep, change, flip" method.
-
Confusing division with subtraction or addition: Clearly understand the operation you're performing; division is different from other arithmetic operations.
Mastering Fraction Division: Tips and Practice
To master fraction division, consistent practice is key. Here are some tips to improve your understanding and skills:
-
Start with simpler examples: Begin with easier problems and gradually increase the complexity.
-
Visualize the problem: Use diagrams or real-world objects to understand the concept more intuitively.
-
Use multiple methods: Try different approaches to solve the same problem; this strengthens understanding and helps identify preferred methods.
-
Practice regularly: Consistent practice builds familiarity and confidence.
Conclusion: Embracing the Power of Fractions
While the initial question, "What is 4 divided by 1/2?", might seem simple, it unveils a world of mathematical concepts and practical applications. Understanding fraction division goes beyond simply arriving at the answer (8); it's about grasping the underlying principles, building a strong mathematical foundation, and applying this knowledge to solve real-world problems effectively. By embracing different solution methods and practicing regularly, you can master fraction division and unlock its power in various aspects of life. Remember the "keep, change, flip" method, visualize the problem, and practice regularly to truly solidify your understanding of this important mathematical concept.
Latest Posts
Latest Posts
-
Born In September 1996 How Old Are You
May 24, 2025
-
Highest Common Factor Of 4 And 8
May 24, 2025
-
How Long Was 17 Years Ago
May 24, 2025
-
7 8 Divided By 2 As A Fraction
May 24, 2025
-
If Your Born 1996 How Old Are You
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.