What Is 2/3 Divided By 4/5
listenit
May 24, 2025 · 5 min read
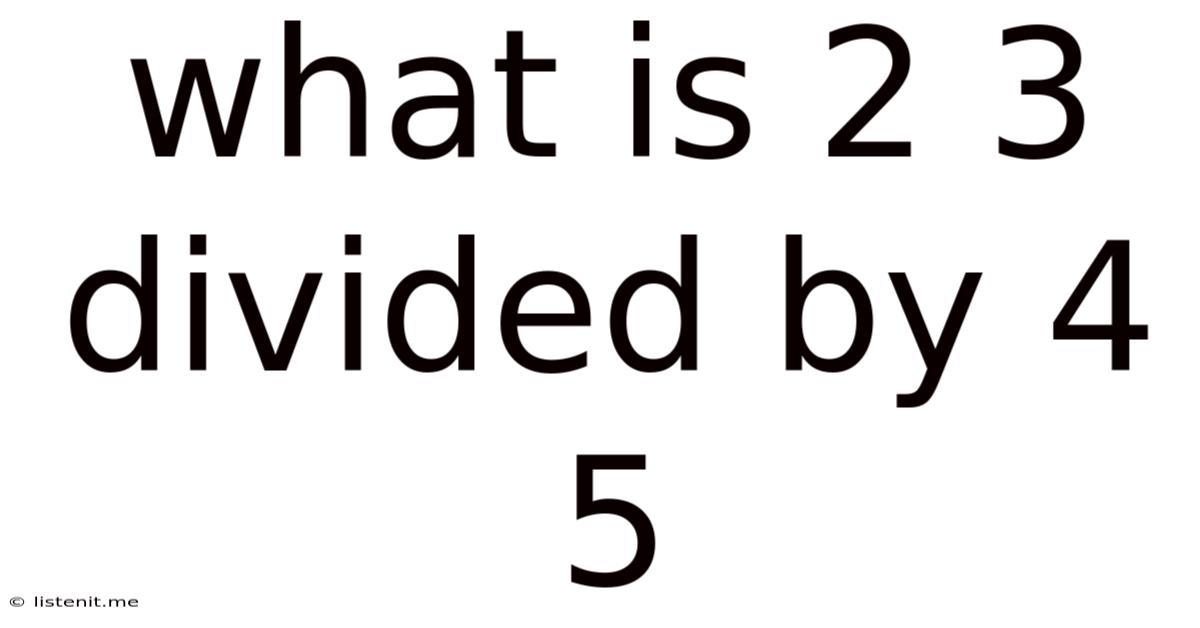
Table of Contents
What is 2/3 Divided by 4/5? A Deep Dive into Fraction Division
Understanding fraction division can seem daunting at first, but with a clear explanation and some practice, it becomes straightforward. This article will not only answer the question "What is 2/3 divided by 4/5?" but also provide a comprehensive understanding of the concept, exploring various methods and tackling common misconceptions. We’ll delve into the intricacies of fraction division, equipping you with the knowledge to confidently tackle similar problems.
Understanding Fraction Division: The Basics
Before we tackle the specific problem of 2/3 divided by 4/5, let's establish a solid foundation in fraction division. The core concept involves finding out how many times one fraction fits into another. Unlike multiplying fractions, where we simply multiply numerators and denominators, division requires a slightly different approach.
The most common and effective method is to invert the second fraction (the divisor) and then multiply. This is often summarized as "Keep, Change, Flip" (KCF):
- Keep: Keep the first fraction as it is.
- Change: Change the division sign to a multiplication sign.
- Flip: Flip (invert) the second fraction. This means swapping the numerator and the denominator.
Solving 2/3 Divided by 4/5: A Step-by-Step Guide
Now, let's apply this method to our problem: 2/3 ÷ 4/5
-
Keep: We keep the first fraction, 2/3, unchanged.
-
Change: We change the division sign (÷) to a multiplication sign (×).
-
Flip: We flip the second fraction, 4/5, to become 5/4.
This transforms our problem into: (2/3) × (5/4)
-
Multiply: Now, we multiply the numerators together and the denominators together:
(2 × 5) / (3 × 4) = 10/12
-
Simplify: Finally, we simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 10 and 12 is 2. Dividing both the numerator and the denominator by 2, we get:
10/12 = 5/6
Therefore, 2/3 divided by 4/5 is 5/6.
Alternative Methods: Visualizing Fraction Division
While the "Keep, Change, Flip" method is efficient, it's helpful to understand the underlying concept. Visualizing fraction division can provide a more intuitive grasp.
Imagine you have 2/3 of a pizza. You want to divide this 2/3 into portions that are each 4/5 of a whole pizza. How many such portions can you make? This visual representation highlights the challenge of dividing a smaller fraction (2/3) by a larger fraction (4/5). The answer, 5/6, indicates that you can make slightly less than a full portion from your 2/3 of a pizza.
Common Mistakes to Avoid
Several common pitfalls can lead to incorrect answers in fraction division. Let's address some of them:
-
Forgetting to invert the second fraction: This is perhaps the most frequent mistake. Remember the "Keep, Change, Flip" rule religiously.
-
Incorrect simplification: Always simplify the resulting fraction to its lowest terms. Failure to do so can lead to an answer that is technically correct but not fully simplified.
-
Confusing division with subtraction or addition: Fraction division is distinct from fraction subtraction or addition. These operations have different rules and procedures.
-
Not understanding the concept: A thorough understanding of what fraction division represents is crucial. If you don't grasp the concept, the mechanical application of rules may lead to errors.
Expanding on Fraction Division: More Complex Examples
Let's explore some more complex examples to solidify your understanding of fraction division:
Example 1: Mixed Numbers
What is 1 1/2 divided by 2 1/3?
First, convert the mixed numbers into improper fractions:
1 1/2 = 3/2 2 1/3 = 7/3
Then apply the "Keep, Change, Flip" method:
(3/2) ÷ (7/3) = (3/2) × (3/7) = 9/14
Example 2: Dividing by a Whole Number
What is 3/4 divided by 2?
Remember that a whole number can be expressed as a fraction with a denominator of 1:
2 = 2/1
Therefore, the problem becomes:
(3/4) ÷ (2/1) = (3/4) × (1/2) = 3/8
Example 3: Dividing Fractions with Larger Numerators and Denominators
What is 15/22 divided by 25/33?
Applying the "Keep, Change, Flip" method:
(15/22) ÷ (25/33) = (15/22) × (33/25) = (15 × 33) / (22 × 25) = 495/550
Simplifying by finding the greatest common divisor (GCD) of 495 and 550 (which is 55):
495/550 = 9/10
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has many practical applications in real-world scenarios:
-
Cooking and Baking: Adjusting recipes to serve more or fewer people often involves fraction division.
-
Sewing and Crafting: Calculating fabric requirements and cutting materials accurately requires precise fraction division.
-
Construction and Engineering: Precise measurements and material calculations in construction rely heavily on fraction division.
-
Data Analysis: Interpreting and manipulating data frequently involves working with fractions and performing division operations.
Conclusion: Mastering Fraction Division
Mastering fraction division is a crucial step in developing a strong mathematical foundation. By understanding the underlying concept, employing the "Keep, Change, Flip" method effectively, and practicing with various examples, you can confidently tackle any fraction division problem. Remember to avoid common mistakes, simplify your answers, and appreciate the versatility of this mathematical skill in various real-world applications. The seemingly complex task of dividing fractions becomes manageable with consistent practice and a firm grasp of the fundamental principles. Keep practicing, and you'll soon find yourself adept at tackling these calculations with ease.
Latest Posts
Latest Posts
-
How Much Is A Car After Taxes
May 25, 2025
-
4 7 8 As An Improper Fraction
May 25, 2025
-
What Is 20 Percent Of 120000
May 25, 2025
-
Gcf Of 10 15 And 30
May 25, 2025
-
3 4 Divided By 7 12
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Divided By 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.