What Is 2 1/4 As A Fraction
listenit
May 09, 2025 · 5 min read
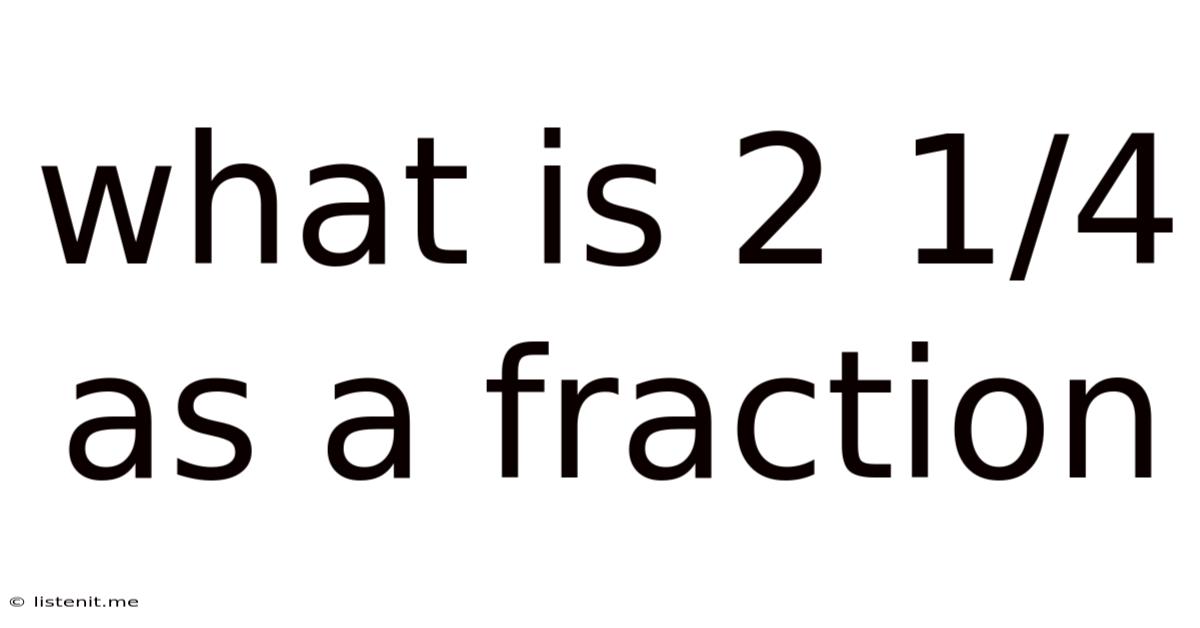
Table of Contents
What is 2 1/4 as a Fraction? A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific concepts. This comprehensive guide delves into the conversion of mixed numbers, like 2 1/4, into improper fractions, explaining the process step-by-step and exploring related concepts. We'll also touch upon the practical applications of this conversion and offer tips for mastering fraction manipulation.
Understanding Mixed Numbers and Improper Fractions
Before we delve into the conversion of 2 1/4, let's first clarify the terminology.
-
Mixed Number: A mixed number combines a whole number and a fraction, like 2 1/4. It represents a quantity that's greater than one.
-
Improper Fraction: An improper fraction has a numerator (the top number) that is greater than or equal to its denominator (the bottom number). For instance, 9/4 is an improper fraction.
Converting a mixed number to an improper fraction is a common task in mathematics, particularly useful when performing operations like addition, subtraction, multiplication, and division involving fractions. The process simplifies calculations and avoids the complexities of working directly with mixed numbers.
Converting 2 1/4 to an Improper Fraction: A Step-by-Step Guide
The conversion of 2 1/4 to an improper fraction involves a straightforward two-step process:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 2, and the denominator of the fraction is 4. Multiplying these together gives us: 2 * 4 = 8
Step 2: Add the result to the numerator.
The numerator of our fraction is 1. Adding the result from Step 1 (8) to the numerator (1) gives us: 8 + 1 = 9
Step 3: Write the result over the original denominator.
The original denominator remains unchanged. Therefore, the improper fraction equivalent of 2 1/4 is 9/4.
This method works for any mixed number. Let's solidify this understanding with another example: convert 3 2/5 to an improper fraction.
- Multiply the whole number by the denominator: 3 * 5 = 15
- Add the result to the numerator: 15 + 2 = 17
- Write the result over the original denominator: 17/5
Therefore, 3 2/5 is equivalent to the improper fraction 17/5.
Why is Converting to Improper Fractions Important?
The conversion of mixed numbers to improper fractions is crucial for several reasons:
-
Simplifying Calculations: Adding, subtracting, multiplying, and dividing fractions is significantly easier when working with improper fractions. Trying to perform these operations directly with mixed numbers often leads to more complex and error-prone calculations.
-
Consistency: Using improper fractions ensures consistency in mathematical operations. It streamlines the process and reduces the possibility of mistakes.
-
Solving Equations: Many mathematical equations and problems require working with fractions. Converting mixed numbers to improper fractions is often a necessary first step in finding solutions.
-
Applications in Real-World Problems: Numerous real-world scenarios involve fractions. From measuring ingredients in cooking to calculating distances or proportions in construction, the ability to convert between mixed numbers and improper fractions is essential.
Practical Applications of 9/4 (2 1/4)
The fraction 9/4, or its mixed number equivalent 2 1/4, has practical applications in various fields:
-
Cooking and Baking: Recipes often require fractional measurements. 2 1/4 cups of flour, for instance, is easily understood as 9/4 cups, simplifying calculations when doubling or halving recipes.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Representing dimensions as improper fractions improves accuracy and simplifies calculations.
-
Finance: Calculating interest, proportions, or shares often involves working with fractions. Converting between mixed numbers and improper fractions helps in these calculations.
-
Data Analysis: In statistical analysis or data representation, using improper fractions can simplify calculations and data interpretations.
Mastering Fraction Manipulation: Tips and Tricks
Mastering fraction manipulation requires practice and a solid understanding of fundamental concepts. Here are some helpful tips:
-
Practice Regularly: Consistent practice is key to improving your skills in working with fractions. Solve various problems involving addition, subtraction, multiplication, and division of fractions.
-
Use Visual Aids: Diagrams and visual representations can help in understanding fraction concepts, especially for beginners.
-
Simplify Fractions: Always simplify fractions to their lowest terms. This makes calculations easier and improves understanding.
-
Understand Equivalent Fractions: Recognizing equivalent fractions (fractions that represent the same value, such as 1/2 and 2/4) is vital for performing operations effectively.
-
Use Online Resources: Many online resources offer interactive exercises and tutorials to improve your understanding and skills in working with fractions.
Beyond the Basics: Exploring Further Concepts
While the conversion of 2 1/4 to 9/4 is a fundamental concept, exploring further mathematical concepts related to fractions can enhance your overall understanding:
-
Decimal Conversions: Learning to convert fractions to decimals and vice-versa broadens your mathematical skills. 9/4, for example, is also equivalent to 2.25.
-
Percentage Conversions: Understanding how to convert fractions to percentages is also beneficial. 9/4 is equivalent to 225%.
-
Fraction Operations: Mastering addition, subtraction, multiplication, and division of fractions is essential for more advanced mathematical applications.
Conclusion: A Solid Foundation in Fractions
Understanding the conversion of mixed numbers, such as 2 1/4, into improper fractions (9/4) is a fundamental building block in mathematics. This seemingly simple conversion has significant practical implications across various fields, from cooking to engineering. Mastering this skill, along with other fraction manipulation techniques, will significantly enhance your mathematical abilities and problem-solving capabilities. Regular practice, the use of visual aids, and exploring further concepts will help you build a solid foundation in working with fractions. Remember, the key is consistent practice and a dedication to understanding the underlying principles.
Latest Posts
Latest Posts
-
D Dx 1 1 X 2
May 09, 2025
-
Difference Between Closed And Open System
May 09, 2025
-
A Fish Tank Is In The Shape Of A Cube
May 09, 2025
-
How To Write Abbreviated Electron Configuration
May 09, 2025
-
How Are All Of The Isotopes Of An Element Similar
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 1/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.