D Dx 1 1 X 2
listenit
May 09, 2025 · 5 min read
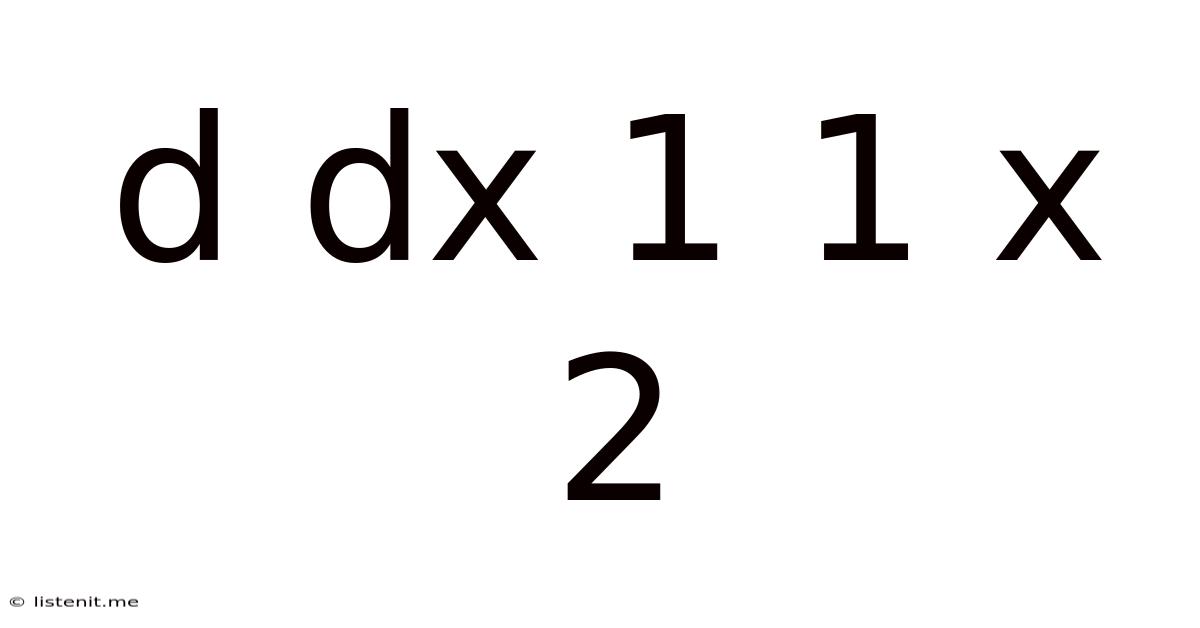
Table of Contents
Demystifying the Derivative: A Deep Dive into d/dx (1/(1+x²))
The expression d/dx (1/(1+x²)) represents the derivative of the function f(x) = 1/(1+x²) with respect to x. This seemingly simple function hides a surprising depth, connecting to fundamental concepts in calculus, trigonometry, and even advanced physics. This article will meticulously explore this derivative, delving into its calculation, its significance, and its applications.
Understanding the Fundamentals: Derivatives and Differentiation
Before tackling the specific derivative, let's refresh our understanding of core calculus concepts. The derivative, denoted by d/dx, measures the instantaneous rate of change of a function. Geometrically, it represents the slope of the tangent line to the function's graph at a given point. The process of finding the derivative is called differentiation.
Several methods exist for differentiating functions. The most fundamental is the limit definition of the derivative:
f'(x) = lim (h→0) [(f(x+h) - f(x))/h]
This formula calculates the slope of the secant line between two points on the curve as the distance between the points approaches zero, yielding the slope of the tangent line. While powerful, this method can be cumbersome for complex functions.
For simpler functions, such as polynomials and rational functions (ratios of polynomials), we can utilize differentiation rules. These rules provide efficient shortcuts for finding derivatives without resorting to the limit definition. Key rules include:
- Power Rule:
d/dx (xⁿ) = nxⁿ⁻¹ - Sum/Difference Rule:
d/dx [f(x) ± g(x)] = f'(x) ± g'(x) - Product Rule:
d/dx [f(x)g(x)] = f'(x)g(x) + f(x)g'(x) - Quotient Rule:
d/dx [f(x)/g(x)] = [f'(x)g(x) - f(x)g'(x)]/[g(x)]² - Chain Rule:
d/dx [f(g(x))] = f'(g(x))g'(x)
Calculating the Derivative: Applying the Quotient Rule
Our target function, f(x) = 1/(1+x²), is a rational function. Therefore, the quotient rule is the most straightforward approach to find its derivative.
Let's break down the application of the quotient rule:
-
Identify f(x) and g(x): In our case,
f(x) = 1andg(x) = 1 + x². -
Find the derivatives of f(x) and g(x):
f'(x) = d/dx (1) = 0(The derivative of a constant is always zero.)g'(x) = d/dx (1 + x²) = 2x(Applying the power rule and sum rule)
-
Apply the quotient rule formula:
f'(x) = [f'(x)g(x) - f(x)g'(x)]/[g(x)]²Substituting our values:
f'(x) = [(0)(1 + x²) - (1)(2x)]/(1 + x²)²Simplifying:
f'(x) = -2x/(1 + x²)²
Therefore, the derivative of 1/(1+x²) with respect to x is -2x/(1 + x²)².
Significance and Applications: Beyond the Calculation
The derivative -2x/(1 + x²)² isn't just a mathematical result; it holds significant implications across various fields.
1. Connection to the Arctangent Function
One of the most crucial aspects of this derivative lies in its integral. The indefinite integral of -2x/(1 + x²)² is directly related to the arctangent function, denoted as arctan(x) or tan⁻¹(x).
The integral represents the area under the curve of the derivative. Knowing this derivative is essential for solving integrals involving this function, a frequent occurrence in many areas of mathematics and physics.
2. Applications in Physics and Engineering
The function 1/(1+x²), and consequently its derivative, appears frequently in physics and engineering problems. Some examples include:
-
Probability Distributions: The Cauchy distribution, a probability distribution with heavy tails, utilizes this function in its probability density function. The derivative is crucial for analyzing various statistical properties of this distribution.
-
Electromagnetism: The function describes aspects of electric and magnetic fields, especially in scenarios involving point charges or dipoles. The derivative aids in calculating field strength variations.
-
Signal Processing: The function and its derivatives are vital for describing various signal characteristics, including frequency analysis and filter design.
3. Numerical Methods and Approximations
The derivative -2x/(1 + x²)² plays a role in numerical methods used to approximate solutions to equations. For instance, Newton-Raphson method, a powerful iterative technique for finding roots of functions, relies heavily on calculating the derivative at each iteration.
4. Geometry and Curve Analysis
The derivative allows us to analyze the geometric properties of the function 1/(1+x²). By examining the sign of the derivative, we can determine where the function is increasing or decreasing. The points where the derivative is zero indicate potential maxima or minima. The second derivative reveals information about the concavity of the curve.
Advanced Considerations: Exploring Related Concepts
The exploration of d/dx (1/(1+x²)) opens doors to several advanced mathematical concepts.
1. Implicit Differentiation
While we used the quotient rule, the derivative could also be found using implicit differentiation. If we consider the equation y(1+x²) = 1, differentiating both sides with respect to x and solving for dy/dx would yield the same result. This method is beneficial when dealing with implicitly defined functions.
2. Partial Derivatives
In multivariable calculus, if x and y are independent variables, we can examine partial derivatives. The partial derivative with respect to x, treating y as a constant, would still be -2x/(1+x²)². This extends our understanding to functions of several variables.
3. Complex Analysis
The function 1/(1+x²) can be extended to the complex plane. In complex analysis, this function is intimately related to the concept of residues and contour integrals, forming the foundation for complex function theory.
Conclusion: The Richness of a Simple Derivative
The seemingly straightforward calculation of d/dx (1/(1+x²)) unveils a wealth of mathematical connections and applications. From its fundamental role in calculus and its connection to the arctangent function to its significance in diverse fields like physics, engineering, and numerical methods, this derivative demonstrates the power and elegance of mathematical analysis. Understanding this derivative is not merely about mastering a calculation; it is about grasping the deep interconnections between seemingly disparate areas of mathematics and their practical relevance in the real world. Further exploration of these related concepts can lead to a deeper appreciation of the beauty and utility of mathematical concepts.
Latest Posts
Latest Posts
-
How Do You Find Number Of Protons In An Element
May 10, 2025
-
What Is The Difference Between Diameter And Radius
May 10, 2025
-
Evaluate Integral In Terms Of Area
May 10, 2025
-
What Would Happen If Dna Replication Did Not Occur
May 10, 2025
-
Which Particles Account For The Mass Of The Atom
May 10, 2025
Related Post
Thank you for visiting our website which covers about D Dx 1 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.