What Is 15 Percent Of 16
listenit
May 24, 2025 · 5 min read
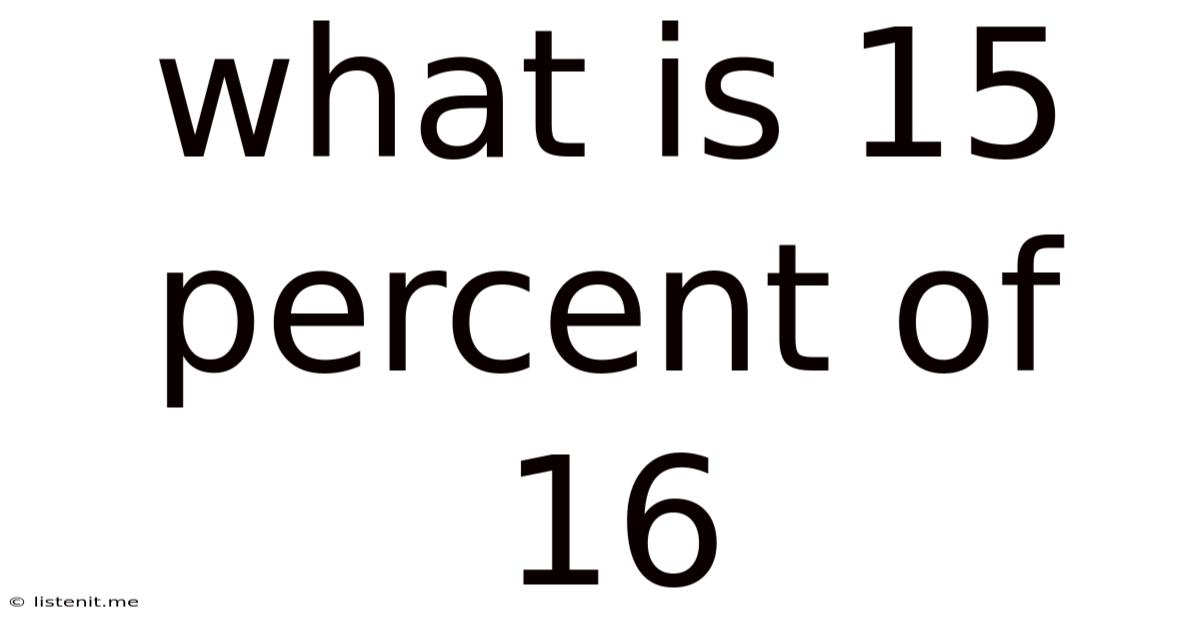
Table of Contents
What is 15 Percent of 16? A Deep Dive into Percentage Calculations
This seemingly simple question, "What is 15 percent of 16?", opens the door to a fascinating exploration of percentages, their applications, and the underlying mathematical principles. While a quick calculation can provide the answer, understanding the how and why behind the calculation is crucial for anyone seeking to confidently navigate the world of percentages. This article will delve deep into this seemingly basic problem, exploring multiple methods of calculation, real-world applications, and even touching upon the history and significance of percentage calculations.
Understanding Percentages: The Foundation
Before jumping into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 15 percent (15%) means 15 out of 100, or 15/100 as a fraction, or 0.15 as a decimal. This foundational understanding is key to solving percentage problems.
Method 1: The Decimal Approach
This is perhaps the most straightforward method for calculating 15% of 16. We convert the percentage to a decimal and then multiply it by the number.
1. Convert the Percentage to a Decimal:
15% = 15/100 = 0.15
2. Multiply the Decimal by the Number:
0.15 * 16 = 2.4
Therefore, 15% of 16 is 2.4
This method is efficient and easily adaptable to various percentage calculations. Its simplicity makes it ideal for quick mental calculations or for use with calculators.
Method 2: The Fraction Approach
This method utilizes the fraction equivalent of the percentage.
1. Convert the Percentage to a Fraction:
15% = 15/100
2. Simplify the Fraction (if possible):
15/100 can be simplified to 3/20
3. Multiply the Fraction by the Number:
(3/20) * 16 = 48/20
4. Simplify the Resulting Fraction:
48/20 simplifies to 12/5, which is equal to 2.4
Therefore, 15% of 16 is 2.4
While slightly more involved than the decimal approach, the fraction method offers a deeper understanding of the underlying mathematical relationships. It's particularly useful when dealing with percentages that have easily simplified fractions.
Method 3: Using Proportions
This method uses the concept of ratios and proportions to solve the problem.
We can set up a proportion:
15/100 = x/16
Where 'x' represents the unknown value (15% of 16). To solve for x, we cross-multiply:
15 * 16 = 100 * x
240 = 100x
x = 240/100
x = 2.4
Therefore, 15% of 16 is 2.4
The proportion method is a powerful tool, especially when dealing with more complex percentage problems or when needing to demonstrate the logical progression of the calculation.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations isn't just about solving math problems; it's about navigating everyday life. Here are some examples:
-
Sales and Discounts: Stores frequently advertise discounts as percentages. Calculating the final price after a 15% discount on a $16 item directly utilizes the concepts discussed above.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Knowing how to calculate these percentages is essential for managing personal finances.
-
Tips and Gratuities: Calculating a tip at a restaurant often involves finding a percentage of the total bill.
-
Interest Rates: Understanding interest rates on loans, savings accounts, and investments requires a firm grasp of percentage calculations.
-
Statistics and Data Analysis: Percentages are ubiquitous in data presentation and interpretation, from analyzing survey results to understanding economic indicators.
-
Scientific Calculations: Many scientific fields, such as chemistry and physics, utilize percentages extensively in calculations and measurements.
-
Financial Markets: Understanding percentage changes in stock prices, bond yields, and other financial instruments is crucial for investors.
Expanding the Concept: Beyond the Basics
While we've focused on calculating 15% of 16, the methods discussed can be applied to any percentage calculation. For instance, finding 37% of 85, 2.5% of 120, or even calculating the percentage one number represents of another, all rely on the fundamental principles detailed above. The key is to systematically convert percentages into decimals or fractions and apply the appropriate multiplication or proportion.
Error Analysis and Troubleshooting
When performing percentage calculations, it's crucial to be mindful of potential errors. Common mistakes include:
-
Incorrect Decimal Conversion: Ensure the percentage is correctly converted to a decimal before multiplication.
-
Calculation Errors: Double-check your multiplication and division to avoid simple arithmetic mistakes.
-
Unit Errors: Always consider the units involved, ensuring consistency throughout the calculation.
-
Misinterpretation of the Problem: Carefully read and understand the problem statement to accurately identify the values to be used in the calculation.
Advanced Percentage Problems and Applications
Beyond basic calculations, there are more complex percentage problems involving consecutive percentages, percentage increases and decreases, and compound interest. These require a deeper understanding of the underlying mathematical concepts but still build upon the foundation established in this article. For example, calculating the final price after multiple discounts (e.g., a 10% discount followed by a 5% discount) requires a step-by-step approach, applying the percentage calculation to the intermediate results.
Conclusion: Mastering Percentages for Everyday Life
In conclusion, the seemingly simple question, "What is 15 percent of 16?" serves as a gateway to a vast and useful area of mathematics. Mastering percentage calculations equips you with a critical skill applicable to countless real-world situations, from personal finance to scientific analysis. By understanding the different calculation methods and potential pitfalls, you can confidently navigate the world of percentages and make informed decisions based on numerical data. Remember to practice regularly and apply the learned concepts to various scenarios to solidify your understanding and improve your efficiency. The more you work with percentages, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
2 Out Of 22 As A Percentage
May 25, 2025
-
5 X 2 3 4x 5
May 25, 2025
-
How Many Usable Ips In A 30
May 25, 2025
-
What Is 1 125 In Fraction Form
May 25, 2025
-
How To Calculate Dollars Per Mile
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.