2 Out Of 22 As A Percentage
listenit
May 25, 2025 · 4 min read
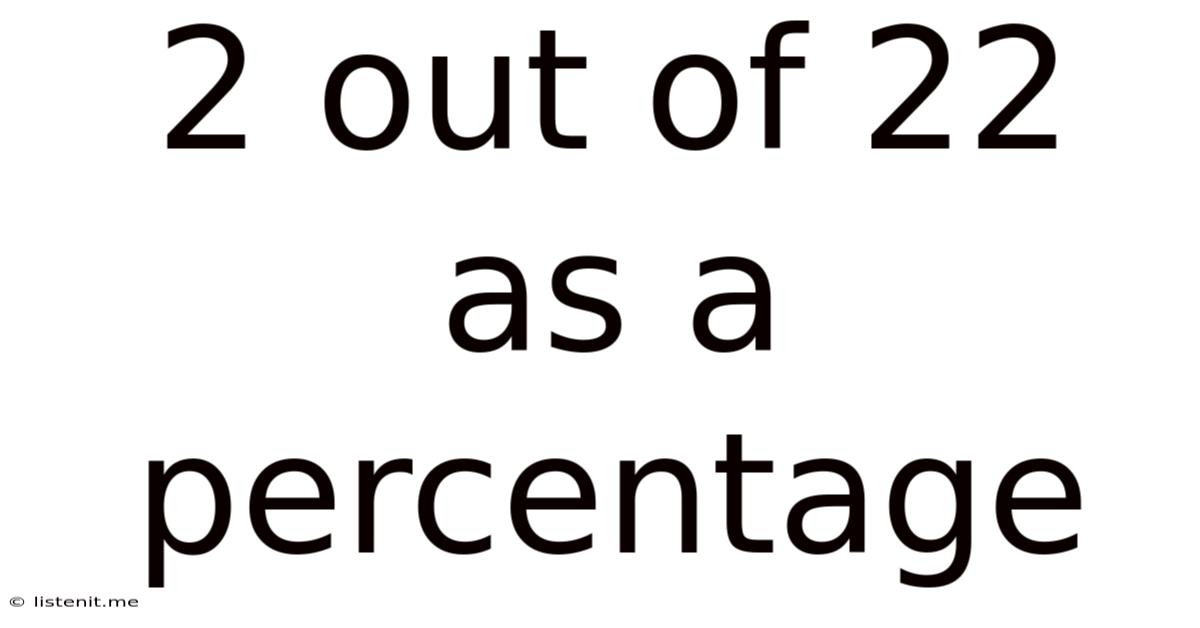
Table of Contents
2 out of 22 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. This comprehensive guide will delve into the calculation of "2 out of 22 as a percentage," explaining the process step-by-step, exploring different calculation methods, and showcasing practical applications. We will also examine related percentage problems and discuss the importance of percentage calculations in various contexts.
Understanding the Basics of Percentages
Before jumping into the specific calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
Calculating 2 out of 22 as a Percentage: The Primary Method
The most straightforward method to calculate 2 out of 22 as a percentage involves the following steps:
-
Express the ratio as a fraction: The statement "2 out of 22" can be written as the fraction 2/22.
-
Convert the fraction to a decimal: Divide the numerator (2) by the denominator (22): 2 ÷ 22 = 0.090909... This decimal is a recurring decimal, meaning the digits 09 repeat infinitely.
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.090909... × 100 = 9.0909...%
-
Round to the desired precision: Depending on the required accuracy, round the percentage. Rounding to two decimal places, we get 9.09%.
Therefore, 2 out of 22 is approximately 9.09%.
Alternative Calculation Methods
While the primary method is quite straightforward, alternative methods can offer a different perspective and might be preferable in certain situations:
-
Simplifying the Fraction: Before converting to a decimal, simplify the fraction 2/22 by dividing both the numerator and denominator by their greatest common divisor, which is 2. This simplifies the fraction to 1/11. Then, divide 1 by 11 (1 ÷ 11 = 0.090909...) and multiply by 100 to get approximately 9.09%.
-
Using Proportions: We can set up a proportion: 2/22 = x/100. To solve for x (the percentage), cross-multiply: 22x = 200. Then, divide both sides by 22: x = 200/22 ≈ 9.09.
Practical Applications of Percentage Calculations
Understanding percentage calculations has wide-ranging practical applications. Consider these examples:
-
Grade Calculations: If a student answers 2 out of 22 questions correctly on a test, their score is approximately 9.09%.
-
Sales and Discounts: If a store offers a discount of 2 out of every 22 items, the discount rate is approximately 9.09%.
-
Statistical Analysis: Percentages are crucial in statistical analysis for representing proportions and trends within datasets.
-
Financial Calculations: Percentage calculations are essential for calculating interest rates, returns on investment, profit margins, and more.
Addressing Common Errors and Misconceptions
When working with percentages, it's crucial to avoid common pitfalls:
-
Rounding Errors: Always be mindful of rounding errors, especially when dealing with recurring decimals. The level of precision depends on the context.
-
Incorrect Fraction Formation: Ensure the fraction is correctly represented. "2 out of 22" is 2/22, not 22/2.
-
Misunderstanding Percentage Change: Percentage change is calculated differently than calculating a percentage from a ratio. Percentage change compares a change in value to the original value.
Expanding on Percentage Concepts: Related Calculations
Let's explore some related percentage calculations that build upon our understanding of "2 out of 22":
-
Finding the Number: If 9.09% of a number is 2, what is the number? We can solve this using the equation: 0.0909x = 2. Solving for x, we get x ≈ 22.
-
Calculating Percentage Increase/Decrease: If the number increases from 2 to 22, the percentage increase is calculated as [(22-2)/2] * 100 = 1000%. If the number decreases from 22 to 2, the percentage decrease is calculated as [(22-2)/22] * 100 ≈ 90.91%.
-
Working with Multiple Percentages: Imagine adding another 2 out of 22. This would be an additional 9.09%, resulting in a total of approximately 18.18% (9.09% + 9.09%).
The Importance of Percentage Calculations in Data Analysis
In the realm of data analysis, percentages provide a standardized and easily interpretable way to represent proportions and trends within large datasets. They allow for efficient comparison across different datasets and facilitate a clear understanding of the relationships between different data points.
Conclusion:
Calculating 2 out of 22 as a percentage, yielding approximately 9.09%, is a seemingly simple calculation but highlights a fundamental concept with far-reaching applications. Mastering percentage calculations is essential for success in numerous fields, from academics and finance to everyday decision-making. By understanding the various methods and avoiding common pitfalls, one can effectively utilize percentages to analyze data, solve problems, and make informed decisions. The ability to perform these calculations confidently is a valuable asset in today’s data-driven world. This guide serves as a foundation for further exploration of percentages and their powerful applications.
Latest Posts
Latest Posts
-
5 Divided By 2 In Fraction Form
May 25, 2025
-
Uk To Us Bra Size Chart
May 25, 2025
-
Least Common Multiple Of 4 8 And 10
May 25, 2025
-
What Percent Of 50 Is 19
May 25, 2025
-
How Many 5 6 Are In 3
May 25, 2025
Related Post
Thank you for visiting our website which covers about 2 Out Of 22 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.