What Is 15 Divided By 1 3
listenit
May 24, 2025 · 5 min read
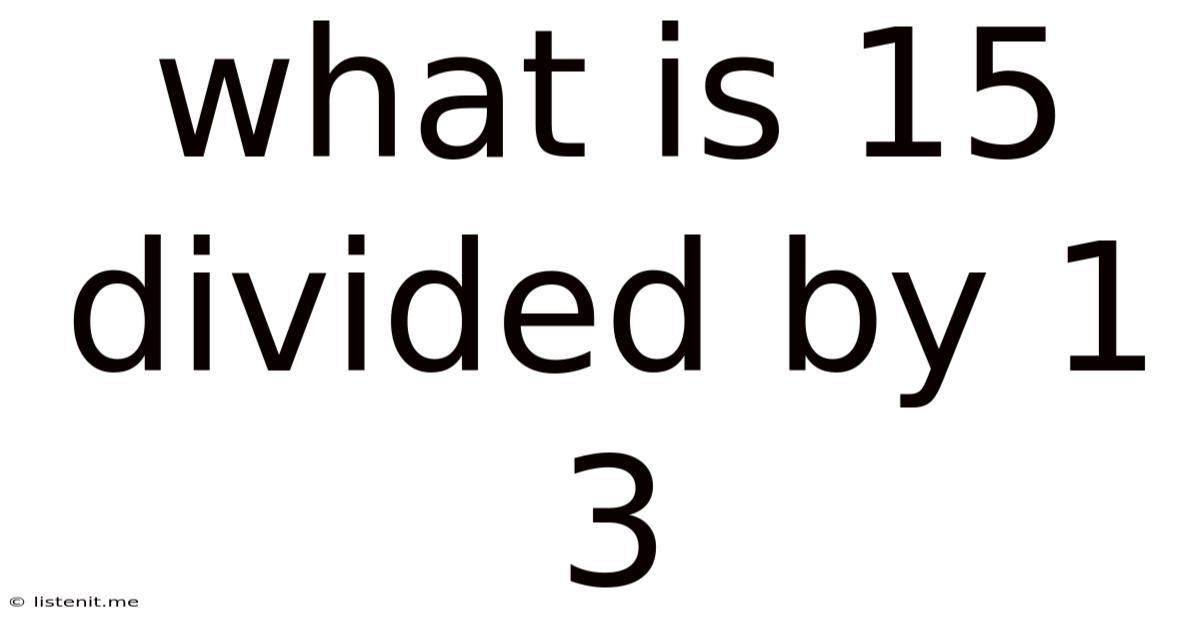
Table of Contents
What is 15 Divided by 1/3? Understanding Fraction Division
The question "What is 15 divided by 1/3?" might seem simple at first glance, but it unveils a fundamental concept in mathematics: fraction division. Understanding this concept is crucial not only for solving this specific problem but also for mastering more complex mathematical operations. This article will thoroughly explore the solution, explain the underlying principles, and provide various approaches to solving similar problems. We will also delve into the practical applications of this type of division and address common misconceptions.
Understanding the Problem: 15 ÷ (1/3)
The problem, 15 ÷ (1/3), asks: "How many times does 1/3 fit into 15?" This phrasing helps to visualize the problem and provides an intuitive approach to solving it. Instead of directly dividing by a fraction, we can reframe the problem using the concept of reciprocals.
The Reciprocal Method: The Easiest Approach
The most straightforward method involves using the reciprocal of the fraction. The reciprocal of a fraction is simply the fraction flipped upside down. The reciprocal of 1/3 is 3/1, or simply 3. To divide by a fraction, we multiply by its reciprocal. Therefore:
15 ÷ (1/3) = 15 × (3/1) = 15 × 3 = 45
Therefore, 15 divided by 1/3 equals 45.
This method is the most efficient and commonly used approach for solving division problems involving fractions. It simplifies the process and avoids the complexities of working directly with fractions in a division context.
Visualizing the Solution
Imagine you have 15 pizzas, and you want to divide them into servings of 1/3 of a pizza each. How many servings can you make? You can make three servings from each pizza, so with 15 pizzas, you can make 15 * 3 = 45 servings. This visual representation reinforces the answer obtained using the reciprocal method.
Alternative Approaches: Exploring Different Methods
While the reciprocal method is the most efficient, let's explore alternative methods to deepen our understanding.
Method 2: Converting to Improper Fractions
We can convert the whole number 15 into a fraction: 15/1. Then, the problem becomes:
(15/1) ÷ (1/3)
When dividing fractions, we multiply the first fraction by the reciprocal of the second fraction:
(15/1) × (3/1) = 45/1 = 45
This method demonstrates the same principle as the reciprocal method but explicitly shows the fractional representation of the whole number, reinforcing the concept of consistent mathematical operations with fractions.
Method 3: Using the Definition of Division
Division can be defined as repeated subtraction. How many times can you subtract 1/3 from 15? While this method is conceptually sound, it's not the most practical for larger numbers. It would involve repeatedly subtracting 1/3 until you reach zero, which would be a tedious process for this specific problem. However, understanding this definition helps solidify the concept of division.
Common Mistakes and Misconceptions
Several common mistakes can occur when working with fraction division:
- Forgetting the reciprocal: The most frequent mistake is simply dividing by the fraction directly instead of multiplying by its reciprocal. Remember, dividing by a fraction is equivalent to multiplying by its inverse.
- Incorrectly simplifying fractions: While simplifying fractions is crucial for accurate calculations, it's important to simplify correctly. Incorrect simplification can lead to an incorrect final answer.
- Confusion with fraction multiplication: Students might sometimes confuse the rules for fraction multiplication with those for fraction division. Remember, division involves multiplying by the reciprocal, not simply multiplying the numerators and denominators.
Practical Applications of Fraction Division
Fraction division is not just an abstract mathematical concept; it has numerous practical applications in various fields:
- Cooking and Baking: Recipes often require fractions of ingredients. Dividing ingredients by fractions is crucial for adjusting recipes for different serving sizes. For example, if a recipe calls for 1/3 cup of sugar, and you want to make three times the recipe, you need to calculate 3 times (1/3 cup), which is 1 cup of sugar.
- Sewing and Crafting: Many crafting projects involve measuring fabrics or other materials in fractions of inches or centimeters. Dividing lengths by fractions is essential for accurate calculations.
- Construction and Engineering: Precision is key in construction and engineering. Calculations involving fractions are common, especially when dealing with measurements and proportions.
- Finance and Business: Fraction division is used extensively in finance and accounting, for example, when calculating proportions of profits or shares.
- Data Analysis and Statistics: Fractions are often encountered when analyzing data and calculating proportions. Dividing by fractions is necessary for understanding relationships between different data points.
Expanding the Concept: Dividing by More Complex Fractions
The principles discussed apply to more complex fraction divisions. For instance:
- Dividing by a mixed number: First, convert the mixed number to an improper fraction, then apply the reciprocal method. For example, 15 divided by 2 1/2 (or 5/2) becomes 15 × (2/5) = 6.
- Dividing by a fraction with a larger numerator than denominator: The same principles apply; find the reciprocal and multiply. For example, 15 divided by 3/2 becomes 15 × (2/3) = 10.
Conclusion: Mastering Fraction Division
Understanding fraction division is essential for anyone working with numbers. While seemingly simple, mastering this concept lays the foundation for tackling more complex mathematical problems. By understanding the reciprocal method and practicing different approaches, you can confidently solve problems involving fractions and apply this knowledge to real-world situations. Remember the crucial step of multiplying by the reciprocal to avoid common mistakes and ensure accuracy. The ability to confidently manipulate fractions will significantly enhance your mathematical skills and problem-solving abilities. Practice makes perfect, so continue working through examples to solidify your understanding and build confidence in your mathematical capabilities.
Latest Posts
Latest Posts
-
15 Is What Percent Of 300
May 24, 2025
-
Greatest Common Factor Of 18 And 81
May 24, 2025
-
What Is A 79 Out Of 100 Grade
May 24, 2025
-
165 As A Fraction In Simplest Form
May 24, 2025
-
What Is 6 Months From August
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.