15 Is What Percent Of 300
listenit
May 24, 2025 · 5 min read
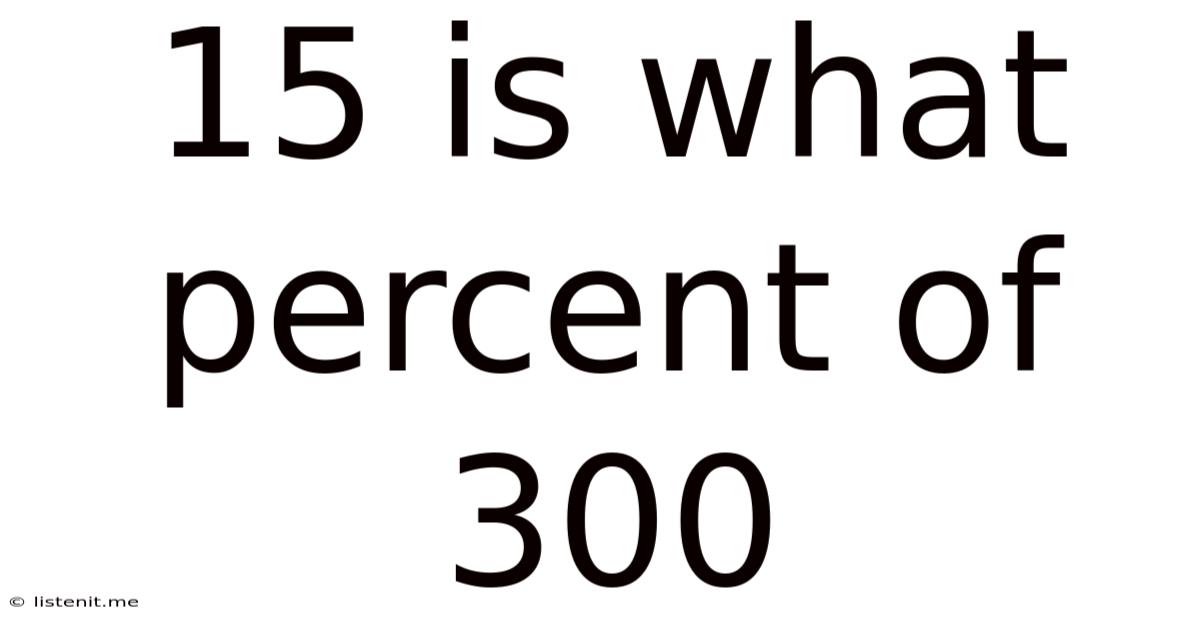
Table of Contents
15 is What Percent of 300? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "15 is what percent of 300?", opens the door to a broader understanding of percentage calculations, a crucial skill in various aspects of life, from everyday budgeting to complex financial analysis. This comprehensive guide will not only answer the question directly but also delve into the underlying concepts, provide multiple approaches to solving the problem, and explore practical applications of percentage calculations.
Understanding Percentages: The Foundation
Before tackling the specific problem, let's establish a solid foundation in understanding percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Key Components of Percentage Problems:
- Part: This represents the smaller portion of the whole. In our problem, 15 is the part.
- Whole: This represents the total amount or the larger quantity. In our problem, 300 is the whole.
- Percentage: This represents the proportional relationship between the part and the whole, expressed as a number out of 100. This is what we need to find.
Method 1: The Formula Approach
The most straightforward method for solving percentage problems involves using a simple formula:
(Part / Whole) * 100 = Percentage
Let's plug in the values from our problem:
(15 / 300) * 100 = Percentage
- Divide the part by the whole: 15 / 300 = 0.05
- Multiply the result by 100: 0.05 * 100 = 5
Therefore, 15 is 5% of 300.
Method 2: The Proportion Method
This method uses the concept of proportions to solve the problem. We can set up a proportion where we equate two ratios:
Part / Whole = Percentage / 100
Let's plug in the values:
15 / 300 = x / 100
Where 'x' represents the percentage we need to find. To solve for x, we can cross-multiply:
15 * 100 = 300 * x
1500 = 300x
Now, divide both sides by 300:
x = 1500 / 300 = 5
Again, we find that 15 is 5% of 300.
Method 3: Using Decimal Equivalents
This method utilizes the understanding that percentages can be expressed as decimals. To convert a percentage to a decimal, simply divide the percentage by 100. Conversely, to convert a decimal to a percentage, multiply the decimal by 100.
In our case, we can express the problem as:
0.05 * 300 = 15
We know that 5% is equal to 0.05 (5/100). Multiplying this decimal by 300 gives us 15, confirming our previous results.
Practical Applications of Percentage Calculations
Understanding percentage calculations is invaluable in a multitude of real-world scenarios. Here are a few examples:
1. Financial Calculations:
- Interest Rates: Calculating simple and compound interest rates heavily relies on percentage calculations.
- Discounts: Determining the final price of an item after a discount involves calculating the percentage discount.
- Taxes: Calculating sales tax, income tax, and other forms of taxes involves percentage calculations.
- Investment Returns: Evaluating the performance of investments and understanding return on investment (ROI) necessitates working with percentages.
- Profit Margins: Businesses use percentage calculations to determine their profit margins – the percentage of profit relative to revenue.
2. Data Analysis and Interpretation:
- Statistical Analysis: Percentages are frequently used to represent data in charts, graphs, and reports, making it easier to understand and interpret trends.
- Surveys and Polls: Results from surveys and polls are often expressed as percentages to show the proportion of respondents choosing a particular option.
- Market Research: Businesses use percentages to analyze market trends, understand customer preferences, and make informed decisions.
3. Everyday Life:
- Tipping: Calculating a tip in a restaurant often involves a percentage calculation (e.g., 15% or 20% of the bill).
- Sales and Promotions: Determining the savings during sales or promotions requires understanding percentages.
- Cooking and Baking: Recipes often use percentages to specify ingredient amounts (e.g., 5% salt by weight).
Beyond the Basics: More Complex Percentage Problems
While the problem "15 is what percent of 300?" is relatively simple, the principles can be extended to more complex scenarios. Consider these variations:
- Finding the Whole: If you know the part and the percentage, you can calculate the whole. For example: "15 is 5% of what number?" This would involve rearranging the formula.
- Finding the Part: If you know the whole and the percentage, you can calculate the part. For example: "What is 5% of 300?" This directly uses the formula.
- Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values, then expressing that difference as a percentage of the original value. For example, finding the percentage increase in sales from one year to the next.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use Different Methods: Try different approaches (formula, proportion, decimal) to find the method you find most intuitive.
- Break Down Complex Problems: Divide complex problems into smaller, manageable steps.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Utilize Online Calculators (for verification, not as a primary method): While calculators can be helpful for verification, it's crucial to understand the underlying principles to solve problems independently.
Conclusion
The ability to perform percentage calculations effectively is a fundamental skill with far-reaching applications. Understanding the underlying concepts, mastering various solution methods, and practicing regularly will equip you to tackle various percentage-related problems confidently and accurately, whether it's calculating a tip, analyzing financial data, or solving more complex mathematical scenarios. The seemingly straightforward question, "15 is what percent of 300?" serves as an excellent starting point for developing a strong understanding of percentages and their widespread utility. Remember to practice consistently, and you'll quickly become proficient in this essential skill.
Latest Posts
Latest Posts
-
How To Calculate Semi Monthly Pay Hourly
May 25, 2025
-
600 Is How Many Times As Much As 20
May 25, 2025
-
What Is The Least Common Multiple Of 15 And 8
May 25, 2025
-
How Many Days Has It Been Since May 12
May 25, 2025
-
What Year Were You Born If You Are 28
May 25, 2025
Related Post
Thank you for visiting our website which covers about 15 Is What Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.