What Is 10 Out Of 12 As A Percentage
listenit
May 25, 2025 · 4 min read
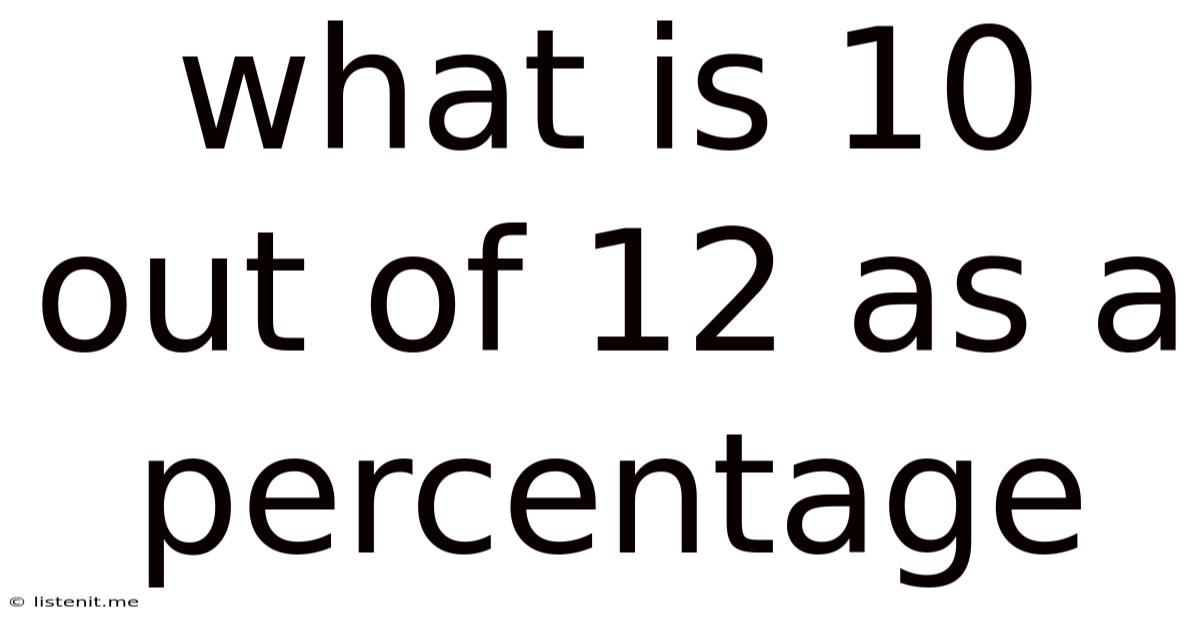
Table of Contents
What is 10 out of 12 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from finance and academics to everyday life. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating effectively. This comprehensive guide will delve into how to calculate "10 out of 12 as a percentage," explaining the process step-by-step, providing alternative methods, and exploring practical applications.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: The Direct Conversion Method
This method involves directly converting the fraction "10 out of 12" into a percentage.
Step 1: Express the Fraction
First, express "10 out of 12" as a fraction: 10/12.
Step 2: Convert to a Decimal
To convert the fraction to a decimal, divide the numerator (10) by the denominator (12):
10 ÷ 12 = 0.8333... (the 3s repeat infinitely)
Step 3: Convert to a Percentage
Multiply the decimal by 100 to express it as a percentage:
0.8333... × 100 = 83.33% (approximately)
Therefore, 10 out of 12 is approximately 83.33%. The repeating decimal can be rounded to the desired level of precision. For most purposes, rounding to two decimal places (83.33%) is sufficient.
Method 2: Simplifying the Fraction First
This method simplifies the fraction before converting it to a percentage, often leading to easier calculations.
Step 1: Simplify the Fraction
Find the greatest common divisor (GCD) of the numerator (10) and the denominator (12). The GCD of 10 and 12 is 2. Divide both the numerator and the denominator by the GCD:
10 ÷ 2 = 5 12 ÷ 2 = 6
This simplifies the fraction to 5/6.
Step 2: Convert to a Decimal
Divide the numerator (5) by the denominator (6):
5 ÷ 6 = 0.8333...
Step 3: Convert to a Percentage
Multiply the decimal by 100:
0.8333... × 100 = 83.33% (approximately)
This method yields the same result: 10 out of 12 is approximately 83.33%. Simplifying the fraction beforehand can make the division easier, especially with larger numbers.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem.
Step 1: Set up a Proportion
We can set up a proportion to find the equivalent percentage:
x/100 = 10/12
Where 'x' represents the percentage we want to find.
Step 2: Cross-Multiply
Cross-multiply the equation:
12x = 1000
Step 3: Solve for x
Divide both sides by 12:
x = 1000/12 = 83.33...
Step 4: Express as a Percentage
Therefore, x ≈ 83.33%, confirming our previous results. This method provides a structured approach, particularly useful when dealing with more complex percentage problems.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages has widespread applications in various contexts:
1. Academic Performance:
Imagine a student scored 10 out of 12 on a quiz. Knowing that this translates to approximately 83.33% helps assess their performance and identify areas for improvement.
2. Financial Calculations:
Businesses frequently use percentages to calculate discounts, profits, taxes, interest rates, and more. For example, a 10% discount on a $120 item would be calculated as (10/100) * $120 = $12.
3. Data Analysis:
Percentages are vital for interpreting statistical data. For example, if a survey shows that 10 out of 12 respondents prefer a particular product, representing 83.33%, this indicates strong preference.
4. Everyday Life:
Calculating tips in restaurants, determining sale prices, or understanding interest on loans all involve percentage calculations.
Advanced Concepts and Considerations
While the basic calculation is straightforward, several nuances can be explored for a deeper understanding:
-
Rounding: As demonstrated, rounding is often necessary when dealing with repeating decimals. The level of precision required depends on the context.
-
Significant Figures: In scientific and engineering applications, the number of significant figures is crucial for accuracy.
-
Percentage Change: This involves calculating the percentage difference between two values, providing insights into growth or decline. For example, if a quantity increases from 12 to 10, the percentage change is calculated as ((10-12)/12)*100% = -16.67%, indicating a decrease.
-
Percentage Point: It is important to differentiate between a percentage change and a percentage point change. A percentage point change refers to the raw difference between two percentages.
Conclusion: Mastering Percentage Calculations
Calculating "10 out of 12 as a percentage" involves a simple yet powerful concept with extensive practical use. This guide has explored three distinct methods, highlighting the versatility of percentage calculations and their relevance across various disciplines. Mastering these techniques empowers you to interpret data effectively, make informed decisions, and communicate quantitative information accurately and confidently. By understanding the underlying principles and applying the appropriate methods, you can navigate the world of percentages with ease and precision. Remember to always consider the context and choose the appropriate level of precision when rounding or presenting your results.
Latest Posts
Latest Posts
-
11 Out Of 23 As A Percentage
May 25, 2025
-
5 Is What Percent Of 17
May 25, 2025
-
12 To The Power Of 0
May 25, 2025
-
1 667 As A Fraction In Simplest Form
May 25, 2025
-
How Many Days Has It Been Since August 8
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Out Of 12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.