11 Out Of 23 As A Percentage
listenit
May 25, 2025 · 5 min read
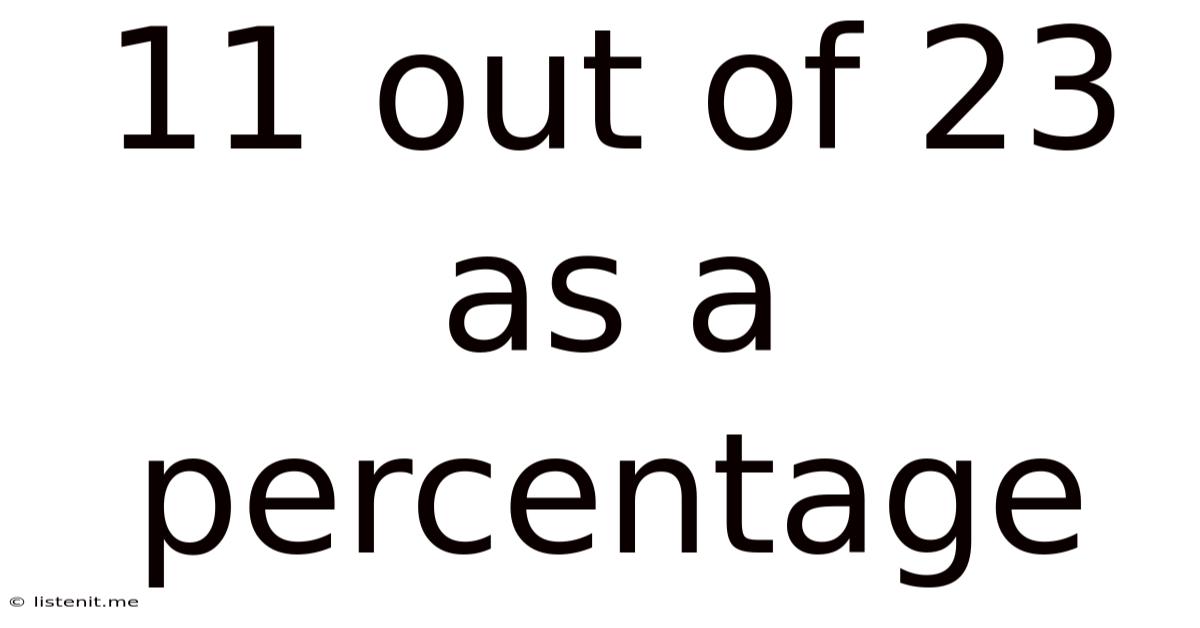
Table of Contents
11 Out of 23 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic pursuits to professional settings. Understanding how to express fractions as percentages is crucial for interpreting data, making informed decisions, and communicating effectively. This comprehensive guide will delve into the intricacies of calculating percentages, specifically focusing on how to determine what 11 out of 23 represents as a percentage, while also providing a broader understanding of percentage calculations and their practical applications.
Understanding Percentages
Before we dive into the specific calculation of 11 out of 23 as a percentage, let's solidify our understanding of what a percentage actually is. A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "per hundred," indicating the proportion of a whole represented by a specific part. For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Key Components of Percentage Calculations
To understand how to calculate percentages effectively, it's essential to grasp the three key components involved:
- The Part: This represents the specific quantity we're interested in expressing as a percentage of the whole. In our case, the part is 11.
- The Whole: This represents the total quantity, the complete amount that the part is a fraction of. In our case, the whole is 23.
- The Percentage: This is the final result, expressed as a number followed by the "%" symbol, indicating the proportional relationship between the part and the whole. This is what we aim to calculate.
Calculating 11 Out of 23 as a Percentage: The Step-by-Step Process
Now, let's calculate what 11 out of 23 represents as a percentage using a simple yet effective method:
-
Form a Fraction: The first step involves expressing the relationship between the part and the whole as a fraction. In this instance, the fraction is 11/23. This fraction indicates that 11 is a part of a larger whole of 23.
-
Convert the Fraction to a Decimal: To convert the fraction to a decimal, we divide the numerator (the top number, 11) by the denominator (the bottom number, 23). Using a calculator or manual division, we get:
11 ÷ 23 ≈ 0.47826
-
Convert the Decimal to a Percentage: The final step involves converting the decimal value to a percentage. To do this, we multiply the decimal by 100 and add the "%" symbol.
0.47826 × 100 ≈ 47.83%
Therefore, 11 out of 23 is approximately 47.83%.
Alternative Calculation Methods
While the method above is straightforward, there are other ways to calculate percentages, each offering advantages depending on the context and your familiarity with mathematical concepts.
Using Proportions
Proportions provide a powerful alternative method, particularly useful for solving more complex percentage problems. We can set up a proportion as follows:
11/23 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
23x = 1100
x = 1100/23 ≈ 47.83
This confirms our previous calculation.
Using Percentage Formula
The percentage formula offers a concise approach to solving percentage problems:
Percentage = (Part/Whole) × 100
Plugging in our values:
Percentage = (11/23) × 100 ≈ 47.83%
This method directly mirrors the steps we took earlier but presents it in a more formalized equation.
Practical Applications of Percentage Calculations
The ability to calculate percentages is a valuable skill with numerous practical applications in diverse fields:
Finance and Budgeting
- Interest Rates: Understanding interest rates on loans, savings accounts, and investments requires accurate percentage calculations.
- Discounts and Sales: Calculating discounts during sales or promotions involves determining the percentage reduction in price.
- Tax Calculations: Income tax, sales tax, and other taxes are often expressed as percentages of income or purchase price.
- Investment Returns: Calculating returns on investments, such as stocks and bonds, relies heavily on percentage calculations.
Data Analysis and Statistics
- Statistical Representation: Percentages are frequently used to present data in a clear and concise manner, such as in charts, graphs, and reports.
- Data Interpretation: Understanding the percentage change between data points allows for insightful analysis of trends and patterns.
- Probability and Statistics: Percentages are essential in expressing probabilities and statistical significance.
Everyday Life
- Tip Calculation: Calculating a tip in a restaurant involves determining a percentage of the total bill.
- Grade Calculation: Academic grades are often expressed as percentages of the total possible points.
- Recipe Scaling: Adjusting recipe ingredients involves calculating percentages to increase or decrease the recipe size.
- Sales Performance: In business, tracking sales performance and growth often involves comparing sales figures as percentages.
Beyond the Basics: Handling More Complex Scenarios
While calculating 11 out of 23 as a percentage is relatively straightforward, many real-world scenarios present more complex challenges. Here are a few examples and how to tackle them:
Percentage Increase and Decrease
Calculating percentage increases or decreases requires understanding the difference between the initial value and the final value. For instance, if a price increases from $100 to $120, the percentage increase is calculated as:
[(120 - 100)/100] × 100 = 20%
Similarly, if a price decreases from $120 to $100, the percentage decrease is:
[(120 - 100)/120] × 100 ≈ 16.67%
Notice the difference: we use the original value as the denominator when calculating percentage change.
Calculating Percentage of a Percentage
Sometimes, you need to calculate a percentage of a percentage. For example, finding 20% of 30% of 1000:
First, find 30% of 1000: 0.3 × 1000 = 300 Then, find 20% of 300: 0.2 × 300 = 60
So, 20% of 30% of 1000 is 60. This is different from simply adding the percentages (50% in this example).
Working with Multiple Percentages
When dealing with multiple percentages applied successively, the order matters. For instance, a 10% discount followed by a 5% discount is not the same as a 15% discount. Each discount is applied to the remaining value.
Conclusion: Mastering Percentage Calculations for Success
The ability to accurately and efficiently calculate percentages is an indispensable skill across many domains. Understanding the underlying principles and various methods for calculation equips individuals with the tools to navigate complex scenarios and make informed decisions in both their personal and professional lives. From financial planning and data analysis to everyday tasks, mastering percentage calculations is a significant step towards achieving greater success and clarity. Remember to always double-check your work, and utilize calculators or spreadsheets when dealing with more intricate calculations. The ability to understand and manipulate percentages is a fundamental building block of numerical literacy and a key component of success in many fields.
Latest Posts
Latest Posts
-
Express The Following Numbers In Scientific Notation
May 25, 2025
-
2 7 1 4 As A Fraction
May 25, 2025
-
What Is 18 Minutes From Now
May 25, 2025
-
Write 8 4 5 As A Decimal Number
May 25, 2025
-
How Much Is A Ps5 After Taxes
May 25, 2025
Related Post
Thank you for visiting our website which covers about 11 Out Of 23 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.