What Is 1 8th Of 24
listenit
May 24, 2025 · 5 min read
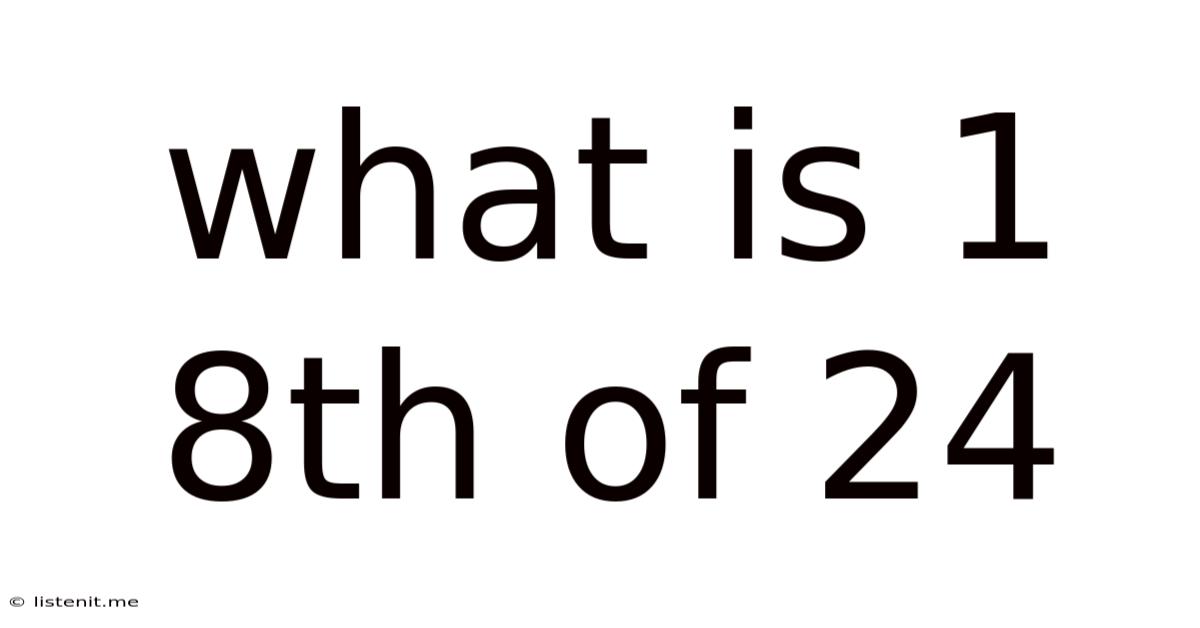
Table of Contents
What is 1/8th of 24? A Deep Dive into Fractions and Their Applications
The seemingly simple question, "What is 1/8th of 24?", opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward, understanding the underlying principles of fractions and their real-world uses provides a richer understanding of mathematics and its relevance in everyday life. This article will not only answer the question but explore the broader context of fractions, their calculations, and their importance across various fields.
Answering the Core Question: 1/8th of 24
To find 1/8th of 24, we need to perform a simple multiplication: (1/8) * 24. This can be solved in a few ways:
-
Method 1: Direct Multiplication: Multiply the numerator (1) by 24 and then divide by the denominator (8): (1 * 24) / 8 = 24 / 8 = 3. Therefore, 1/8th of 24 is 3.
-
Method 2: Simplification Before Multiplication: We can simplify the fraction before multiplying. Since 24 is divisible by 8 (24/8 = 3), we can simplify the expression to: (1/8) * 24 = 1 * (24/8) = 1 * 3 = 3. This method often leads to easier calculations, especially with larger numbers.
-
Method 3: Visual Representation: Imagine dividing a whole (represented by 24 units) into eight equal parts. Each part represents 1/8th of the whole. To find 1/8th of 24, simply determine the value of one of these eight equal parts. 24 divided into 8 equal parts gives us 3 units per part.
Understanding Fractions: A Foundation of Mathematics
Fractions are a fundamental concept in mathematics, representing parts of a whole. They consist of two parts: a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator shows the total number of equal parts the whole is divided into.
Understanding fractions is crucial for various mathematical operations, including:
-
Addition and Subtraction: Adding and subtracting fractions requires a common denominator. This ensures that we are adding or subtracting like units. For example, adding 1/2 and 1/4 requires converting 1/2 to 2/4 before adding, resulting in 3/4.
-
Multiplication and Division: Multiplying fractions involves multiplying the numerators and the denominators separately. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
-
Decimals and Percentages: Fractions can be easily converted to decimals by dividing the numerator by the denominator. Decimals can then be converted to percentages by multiplying by 100. This interchangeability allows for flexibility in mathematical calculations and problem-solving.
Real-World Applications of Fractions: Beyond the Classroom
Fractions are not confined to textbooks; they are integral parts of everyday life, appearing in numerous contexts:
-
Cooking and Baking: Recipes often use fractions to specify ingredient quantities (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt). Understanding fractions ensures accurate measurements and successful cooking outcomes.
-
Measurements and Engineering: Fractions are essential in various measurement systems, from inches and feet to metric units. Engineers and architects use fractions for precise calculations in design and construction.
-
Finance and Budgeting: Fractions are crucial for understanding financial concepts like interest rates, loan payments, and investment returns. They help us manage our personal finances effectively.
-
Data Analysis and Statistics: Fractions are fundamental in representing proportions and probabilities in statistical analysis. They help interpret data and draw meaningful conclusions.
-
Time Management: We often use fractions to represent portions of time (e.g., 1/2 hour, 1/4 of a day). Efficient time management requires understanding and utilizing fractions.
Expanding on the Concept: Exploring Multiples of 1/8th of 24
While we've focused on 1/8th of 24, understanding the concept allows us to easily calculate multiples of this fraction. For example:
-
2/8th of 24: This is simply double 1/8th of 24, which is 2 * 3 = 6.
-
3/8th of 24: This is three times 1/8th of 24, which is 3 * 3 = 9.
-
4/8th of 24: This simplifies to 1/2 of 24, which is 12.
-
5/8th of 24: This is five times 1/8th of 24, which is 5 * 3 = 15.
-
6/8th of 24: This simplifies to 3/4 of 24, which is 18.
-
7/8th of 24: This is seven times 1/8th of 24, which is 7 * 3 = 21.
-
8/8th of 24: This simplifies to the whole, which is 24.
This demonstrates the versatility of fractions and their ability to represent various proportions of a given quantity.
Fractions and Decimal Equivalents: A Seamless Transition
It's important to understand the relationship between fractions and decimals. As mentioned earlier, fractions can be easily converted to decimals by dividing the numerator by the denominator. For instance, 1/8 can be expressed as 0.125. This equivalence allows us to use both forms interchangeably, depending on the context and the required level of precision.
Understanding these equivalencies is vital for various applications, especially when working with computers or calculators that often operate using decimal systems.
Advanced Applications: Fractions in Algebra and Calculus
The concepts of fractions extend far beyond basic arithmetic. They are fundamental building blocks in more advanced mathematical fields like algebra and calculus.
-
Algebra: Fractions are used extensively in algebraic equations and expressions. Manipulating fractional equations requires a deep understanding of fraction operations and algebraic principles.
-
Calculus: Calculus heavily relies on the concepts of limits and derivatives, both of which often involve working with fractions and infinitesimal quantities. Understanding fractions is therefore essential for mastering calculus.
Conclusion: The Importance of Mastering Fractions
The simple question of "What is 1/8th of 24?" serves as a gateway to understanding the pervasive role of fractions in mathematics and its various applications. From everyday tasks like cooking and budgeting to advanced mathematical concepts in algebra and calculus, fractions are essential tools for navigating the world around us. Mastering fractions is not just about solving arithmetic problems; it's about building a strong foundation in mathematics that unlocks numerous opportunities in education, career, and life. By understanding the principles and applications of fractions, we equip ourselves with a powerful tool for problem-solving and critical thinking across various disciplines. Therefore, continuing to explore and deepen our understanding of fractions is a worthwhile intellectual endeavor with practical benefits that extend far beyond the classroom.
Latest Posts
Latest Posts
-
What Is 17 Percent Of 100
May 24, 2025
-
5am To 12am Is How Many Hours
May 24, 2025
-
What Is 2 1 As A Fraction
May 24, 2025
-
What Is 4 Divided By 1 2
May 24, 2025
-
Cash On Cash Return Calculator Real Estate
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 8th Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.