What Is 1/4 Of 3 1/2
listenit
May 23, 2025 · 4 min read
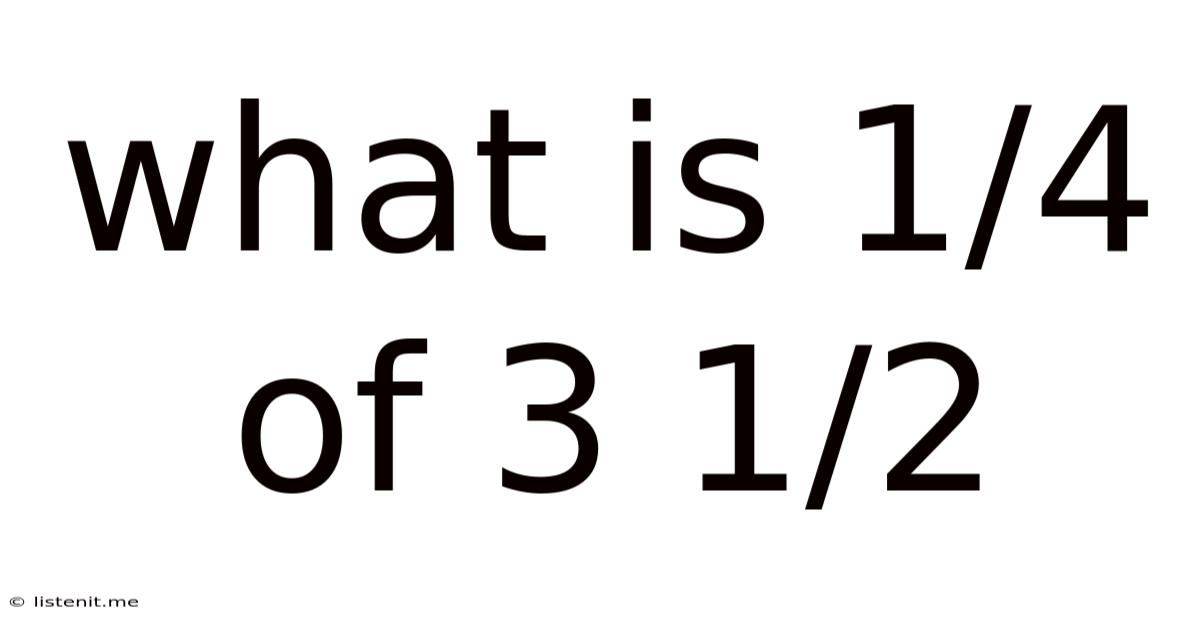
Table of Contents
What is 1/4 of 3 1/2? A Comprehensive Guide to Fraction Multiplication
Finding a fraction of another number, whether a whole number or a fraction, is a fundamental concept in mathematics. Understanding this process is crucial for various applications, from baking and cooking to engineering and finance. This comprehensive guide will walk you through the calculation of 1/4 of 3 1/2, explaining the underlying principles and providing various methods to solve this type of problem. We'll also delve into the practical applications and explore related concepts to solidify your understanding.
Understanding Fractions: A Quick Recap
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/4, the numerator is 1, and the denominator is 4. This means we have 1 part out of a total of 4 equal parts.
Converting Mixed Numbers to Improper Fractions
The number 3 1/2 is a mixed number, meaning it combines a whole number (3) and a fraction (1/2). To perform calculations involving fractions, it's often easier to convert mixed numbers into improper fractions. An improper fraction has a numerator that is greater than or equal to its denominator.
To convert 3 1/2 to an improper fraction:
- Multiply the whole number by the denominator: 3 * 2 = 6
- Add the numerator: 6 + 1 = 7
- Keep the same denominator: The improper fraction is 7/2.
Therefore, 3 1/2 is equivalent to 7/2.
Calculating 1/4 of 3 1/2: Method 1 - Converting to Improper Fractions
Now that we have converted 3 1/2 to 7/2, we can calculate 1/4 of 3 1/2 by multiplying the two fractions:
(1/4) * (7/2) = (1 * 7) / (4 * 2) = 7/8
Therefore, 1/4 of 3 1/2 is 7/8.
Calculating 1/4 of 3 1/2: Method 2 - Working with the Whole Number and Fraction Separately
Alternatively, we can calculate 1/4 of 3 1/2 by working with the whole number and the fraction separately:
- Find 1/4 of the whole number (3): (1/4) * 3 = 3/4
- Find 1/4 of the fraction (1/2): (1/4) * (1/2) = 1/8
- Add the results together: 3/4 + 1/8
To add these fractions, we need a common denominator, which is 8:
3/4 = 6/8
Now, add the fractions:
6/8 + 1/8 = 7/8
Again, we arrive at the answer: 1/4 of 3 1/2 is 7/8.
Visualizing the Calculation
Imagine a pizza cut into 8 slices. 3 1/2 pizzas would represent 7 half-pizzas (since 3 whole pizzas have 6 half-pizzas, plus another half-pizza). If we want to find 1/4 of this amount, we're looking for 1/4 of those 7 half-pizzas. Dividing 7 half-pizzas into 4 equal groups gives you 7/8 of a pizza in each group.
Practical Applications
Understanding fraction multiplication has many practical applications in daily life. Some examples include:
- Cooking and Baking: Recipes often require fractions of ingredients. Calculating 1/4 of a recipe would involve similar fraction multiplication.
- Construction and Engineering: Accurate measurements and calculations are crucial in construction and engineering projects. Fractions are frequently used to ensure precision.
- Finance: Calculating interest, discounts, or shares often involves working with fractions and percentages, which are closely related.
- Data Analysis: When working with datasets, understanding fractions is important for interpreting proportions and percentages.
Expanding on Fraction Operations
This problem highlights the importance of understanding fundamental fraction operations, including:
- Multiplication of fractions: The core operation used to solve this problem. Remember that you multiply the numerators together and the denominators together.
- Conversion between mixed numbers and improper fractions: A crucial step in simplifying calculations.
- Finding common denominators: Necessary when adding or subtracting fractions.
- Simplifying fractions: Reducing a fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Further Exploration: Percentages and Decimals
The result 7/8 can also be expressed as a percentage or a decimal. To convert a fraction to a percentage, multiply it by 100%:
(7/8) * 100% = 87.5%
To convert a fraction to a decimal, divide the numerator by the denominator:
7 ÷ 8 = 0.875
Therefore, 1/4 of 3 1/2 is equivalent to 87.5% or 0.875.
Conclusion
Calculating 1/4 of 3 1/2 involves understanding and applying fundamental principles of fraction manipulation. By converting mixed numbers to improper fractions and employing the rules of fraction multiplication, we arrive at the answer of 7/8, which is equivalent to 87.5% or 0.875. Mastering these concepts is vital for various mathematical applications and real-world scenarios. Remember to practice regularly to solidify your understanding and build confidence in handling fraction problems. The more you practice, the more intuitive these calculations will become. This detailed explanation provides a comprehensive understanding of the process, equipping you with the skills to tackle similar fraction problems confidently.
Latest Posts
Latest Posts
-
What Is 80 000 After Taxes
May 23, 2025
-
What Is 20 Percent Of 76
May 23, 2025
-
6 Is What Percent Of 22
May 23, 2025
-
5 8 Divided By 1 2
May 23, 2025
-
How Many Hours In 12 Years
May 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Of 3 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.