5 8 Divided By 1 2
listenit
May 23, 2025 · 5 min read
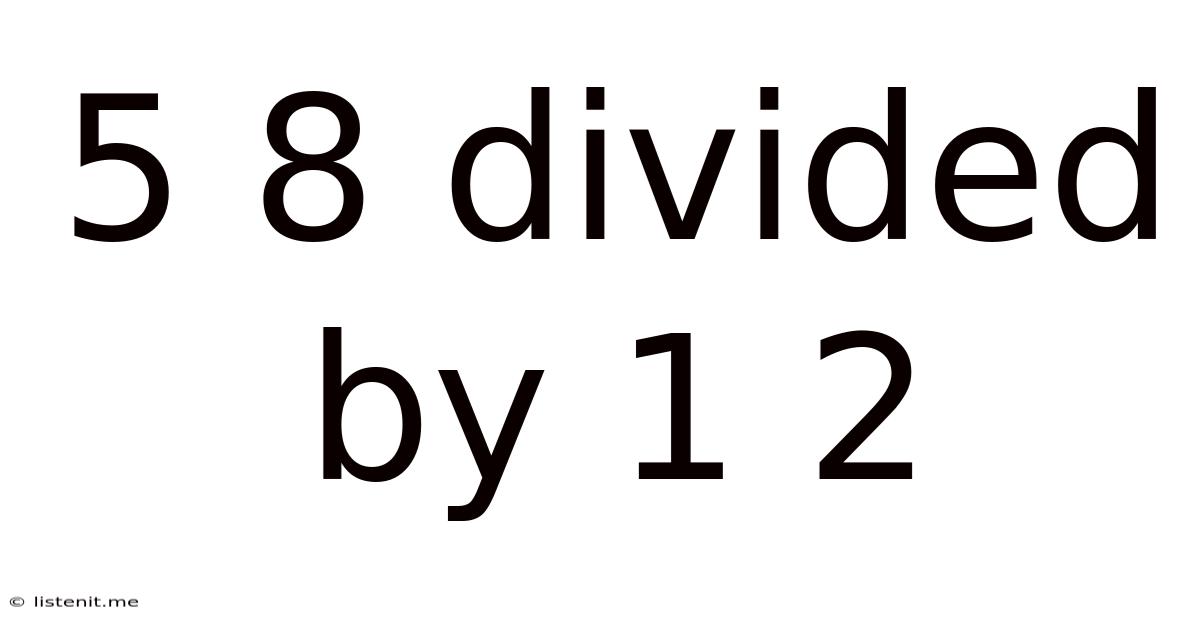
Table of Contents
5/8 Divided by 1/2: A Deep Dive into Fraction Division
This seemingly simple arithmetic problem, 5/8 divided by 1/2, opens a door to a deeper understanding of fraction division, its applications, and the underlying mathematical principles. While the answer itself is straightforward, exploring the why behind the solution reveals crucial concepts vital for mathematical proficiency. This article will not only solve the problem but also illuminate the methods, explain the reasoning, and explore practical applications of fraction division.
Understanding Fraction Division
Before tackling 5/8 divided by 1/2, let's establish a solid foundation in fraction division. Unlike addition or subtraction, division with fractions isn't intuitively obvious. The core concept revolves around the question: "How many times does one fraction fit into another?"
For instance, 5/8 divided by 1/2 asks: "How many times does 1/2 fit into 5/8?" Visualizing this with a pie chart or other graphical representation can be helpful. Imagine a pie cut into eight slices; you possess five of them (5/8). How many times can you take away a half-pie (1/2) from your five slices? This visualization helps to understand that the answer will be a number less than one, as 1/2 is larger than 5/8.
The "Keep, Change, Flip" Method
One of the most common and effective techniques for dividing fractions is the "keep, change, flip" method, also known as the reciprocal method. Here's how it works:
- Keep: Keep the first fraction (the dividend) exactly as it is: 5/8.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) – find its reciprocal. The reciprocal of 1/2 is 2/1 (or simply 2).
Therefore, 5/8 divided by 1/2 becomes: 5/8 × 2/1.
Solving the Problem: 5/8 × 2/1
Now that we've transformed the division problem into a multiplication problem, solving it is straightforward. We multiply the numerators together and the denominators together:
(5 × 2) / (8 × 1) = 10/8
This result, 10/8, is an improper fraction (the numerator is larger than the denominator). To express this in a more conventional way, we simplify it to a mixed number.
Simplifying the Fraction: From Improper to Mixed Number
To convert 10/8 to a mixed number, we divide the numerator (10) by the denominator (8):
10 ÷ 8 = 1 with a remainder of 2.
This means that 10/8 is equal to 1 and 2/8. We can further simplify 2/8 by dividing both the numerator and denominator by their greatest common divisor, which is 2:
2/8 = 1/4
Therefore, the final answer is 1 1/4. This confirms our initial intuition that 1/2 fits into 5/8 a little more than once.
Deeper Dive: Mathematical Principles
The "keep, change, flip" method isn't just a trick; it's a direct consequence of the mathematical definition of division. Division is the inverse operation of multiplication. Dividing by a fraction is equivalent to multiplying by its reciprocal. Let's explore this in more detail:
Dividing by 1/2 is the same as multiplying by 2/1. This is because:
(a ÷ b) = (a × (1/b))
In our case, a = 5/8 and b = 1/2. Therefore:
(5/8) ÷ (1/2) = (5/8) × (2/1) = 10/8 = 1 1/4
Practical Applications of Fraction Division
Understanding fraction division isn't just an academic exercise; it has numerous practical applications across various fields:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 1/2 cup of flour and you want to make only 1/4 of the recipe, you need to calculate (1/2) ÷ (4/1) = 1/8 cup of flour.
-
Sewing and Crafting: Calculating fabric needs, determining yarn amounts for knitting or crocheting, or dividing materials for projects all involve fraction division.
-
Construction and Carpentry: Precise measurements are crucial, and dividing fractions is essential for calculating cuts, proportions, and material needs.
-
Engineering and Design: Scaling blueprints, calculating material strengths, and designing complex systems often involve fractional calculations.
-
Financial Calculations: Dividing fractions is used in areas such as calculating portions of investments, determining interest rates, or analyzing financial statements.
-
Data Analysis: In statistical analysis, data manipulation often includes dividing fractions to normalize data or calculate ratios.
-
Everyday Life: Many everyday tasks implicitly involve fraction division, such as sharing food equally among friends, calculating portions, or measuring ingredients.
Alternative Methods for Dividing Fractions
While the "keep, change, flip" method is popular, other approaches exist, offering alternative ways to understand the concept:
-
Common Denominator Method: Find a common denominator for both fractions and then divide the numerators. This method can be more time-consuming but offers a different perspective on fraction division. In our example, the common denominator for 5/8 and 1/2 is 8. Therefore, 1/2 becomes 4/8. Then we divide the numerators: (5/8) ÷ (4/8) = 5/4 = 1 1/4
-
Visual Representation: Using diagrams like pie charts or number lines can provide a visual understanding of the division process. Drawing 5/8 of a pie and then repeatedly subtracting 1/2 will illustrate how many times 1/2 fits into 5/8.
Conclusion
The seemingly simple problem of 5/8 divided by 1/2 serves as a gateway to a more profound understanding of fraction division. Mastering this concept is not only crucial for academic success but also essential for navigating numerous real-world applications. By understanding the "keep, change, flip" method and its mathematical underpinnings, as well as exploring alternative methods, you can confidently tackle fraction division problems and utilize this fundamental skill in various contexts. Remember that practice is key to mastering any mathematical concept, so continue to work through examples and apply your knowledge to real-world scenarios to solidify your understanding. The ability to effectively work with fractions is a powerful tool that will serve you well in numerous aspects of life.
Latest Posts
Latest Posts
-
What Percent Is 6 Of 16
May 24, 2025
-
What Is 14 As A Fraction
May 24, 2025
-
What Is The Gcf Of 32 And 40
May 24, 2025
-
6pm To 5am Is How Many Hours
May 24, 2025
-
How Many Days Since April 19
May 24, 2025
Related Post
Thank you for visiting our website which covers about 5 8 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.