What Is 1/4 Divided By 3 As A Fraction
listenit
May 09, 2025 · 4 min read
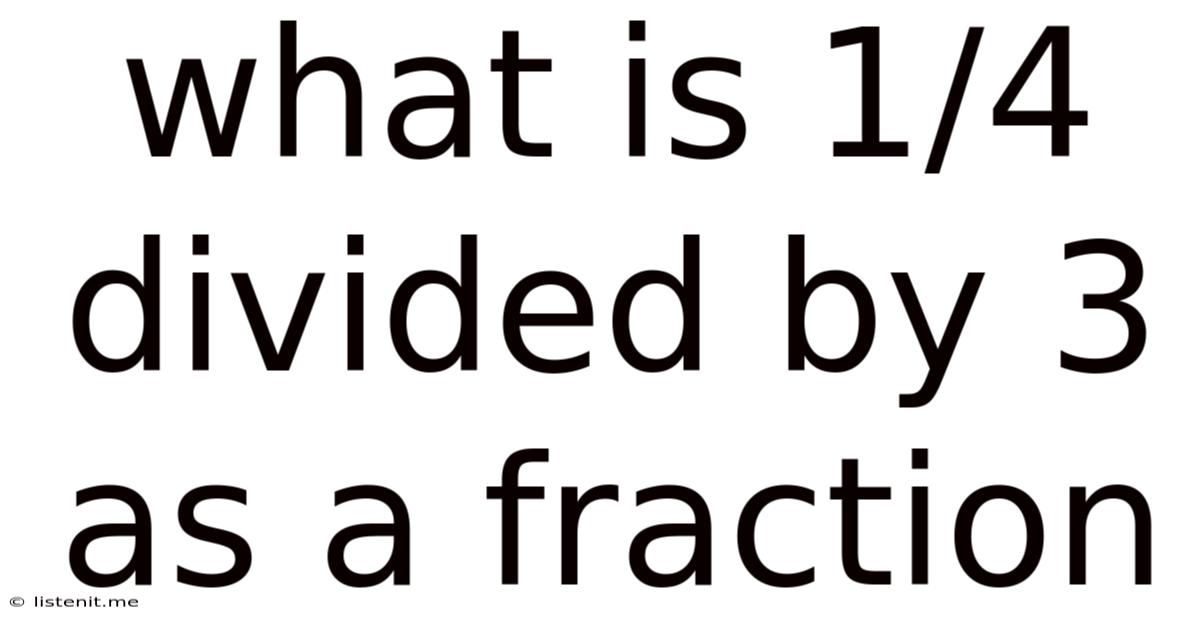
Table of Contents
What is 1/4 Divided by 3 as a Fraction? A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through solving the problem "What is 1/4 divided by 3 as a fraction?", explaining the steps involved and offering additional examples to solidify your understanding of fraction division. We'll also explore the underlying mathematical principles and provide practical applications.
Understanding Fraction Division
Before diving into the specific problem, let's establish a foundational understanding of fraction division. The core concept is to invert the second fraction (the divisor) and multiply. This is equivalent to finding out "how many times the divisor goes into the dividend". This method works because division is the inverse operation of multiplication.
Think of it this way: dividing by 3 is the same as multiplying by 1/3. This is the crucial step that simplifies the process significantly.
Solving 1/4 Divided by 3
Now, let's tackle the specific problem: 1/4 divided by 3. Following the rule of inverting and multiplying:
-
Rewrite the problem: 1/4 ÷ 3 can be rewritten as (1/4) ÷ (3/1). Remember, any whole number can be expressed as a fraction by placing it over 1.
-
Invert the second fraction: The second fraction, 3/1, becomes 1/3.
-
Multiply the fractions: Now we multiply the first fraction by the inverted second fraction: (1/4) * (1/3)
-
Multiply the numerators and denominators: Multiply the numerators together (1 * 1 = 1) and the denominators together (4 * 3 = 12).
-
Simplify the fraction (if possible): The resulting fraction is 1/12. In this case, the fraction is already in its simplest form, meaning there's no common factor (other than 1) that divides both the numerator and denominator.
Therefore, 1/4 divided by 3 is 1/12.
Visualizing the Solution
Visualizing the problem can be helpful in understanding the concept. Imagine you have a pizza cut into four equal slices. 1/4 represents one slice. Dividing this slice into three equal parts means each part is 1/12 of the whole pizza.
More Examples of Fraction Division
Let's reinforce this concept with some additional examples:
Example 1: 2/5 ÷ 4
- Rewrite as a fraction: (2/5) ÷ (4/1)
- Invert the second fraction: 1/4
- Multiply: (2/5) * (1/4) = 2/20
- Simplify: 1/10
Therefore, 2/5 divided by 4 is 1/10.
Example 2: 3/7 ÷ 2/3
- Rewrite: (3/7) ÷ (2/3)
- Invert: 3/2
- Multiply: (3/7) * (3/2) = 9/14
Therefore, 3/7 divided by 2/3 is 9/14.
Example 3: 5/8 ÷ 1/2
- Rewrite: (5/8) ÷ (1/2)
- Invert: 2/1
- Multiply: (5/8) * (2/1) = 10/8
- Simplify: 5/4 or 1 1/4
Therefore, 5/8 divided by 1/2 is 5/4 or 1 1/4.
Practical Applications of Fraction Division
Fraction division isn't just a theoretical concept; it has many practical applications in everyday life and various fields:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you need to divide 1/2 by 2.
-
Sewing and Crafting: Cutting fabric or other materials into specific proportions often involves fraction division.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering frequently require working with fractions.
-
Data Analysis and Statistics: Understanding proportions and ratios in data often necessitates working with fractions and fraction division.
Troubleshooting Common Mistakes
Several common mistakes can occur when dividing fractions. Let's address these to avoid confusion:
-
Forgetting to invert: The most common mistake is forgetting to invert (reciprocate) the second fraction before multiplying. Always remember this crucial step.
-
Incorrect multiplication: After inverting, ensure you correctly multiply the numerators and the denominators.
-
Failure to simplify: Always simplify your final answer to its lowest terms. This makes the answer easier to understand and interpret.
Conclusion
Dividing fractions, while initially appearing complex, becomes manageable with practice and a solid understanding of the underlying principles. By inverting the second fraction and multiplying, you can solve any fraction division problem effectively. Remember to always simplify your answer and practice regularly to build confidence and mastery of this essential mathematical skill. This guide, along with the provided examples and troubleshooting tips, should equip you to tackle any fraction division problem with ease. Remember to always check your work and ensure your answer is in its simplest form. Happy calculating!
Latest Posts
Latest Posts
-
4 Divided By 1 3 In Fraction Form
May 09, 2025
-
Sodium Chloride Silver Nitrate Balanced Equation
May 09, 2025
-
How Many Different Integers Can Have The Same Absolute Value
May 09, 2025
-
Find The Equation Of The Horizontal Line
May 09, 2025
-
13 4 As A Mixed Number
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.