4 Divided By 1 3 In Fraction Form
listenit
May 09, 2025 · 4 min read
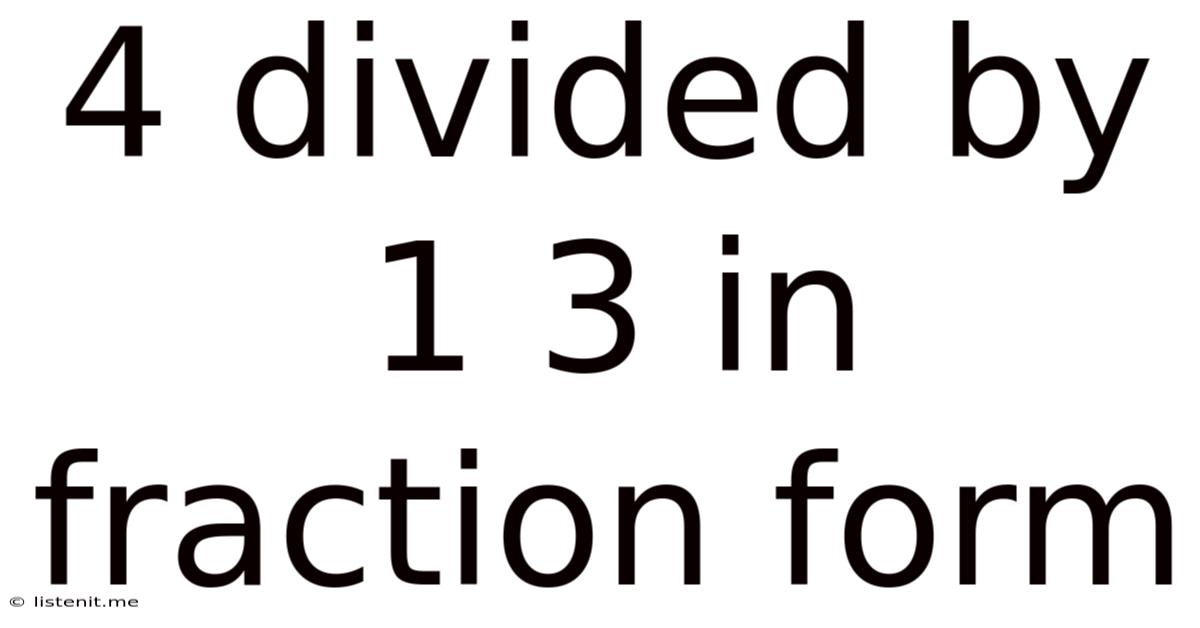
Table of Contents
4 Divided by 1 3/4 in Fraction Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a systematic approach, it becomes manageable. This article delves into the process of dividing 4 by the mixed number 1 3/4, explaining the steps clearly and providing additional insights into fraction manipulation. We'll not only solve the problem but also explore the underlying concepts and offer practice examples to solidify your understanding.
Understanding the Fundamentals: Fractions and Mixed Numbers
Before we tackle the division problem, let's refresh our understanding of fractions and mixed numbers.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator.
Mixed Numbers: A mixed number combines a whole number and a fraction. For instance, 1 3/4 represents one whole unit and three-quarters of another unit. To work with mixed numbers in division, it's often easier to convert them into improper fractions.
Improper Fractions: An improper fraction has a numerator that is greater than or equal to its denominator. For example, 7/4 is an improper fraction. It represents more than one whole unit. Converting mixed numbers to improper fractions is a crucial step in many fraction calculations.
Converting Mixed Numbers to Improper Fractions
To convert a mixed number to an improper fraction, follow these steps:
-
Multiply the whole number by the denominator of the fraction: In the case of 1 3/4, we multiply 1 (the whole number) by 4 (the denominator). This gives us 4.
-
Add the result to the numerator of the fraction: Now, add 4 to the numerator, which is 3. This gives us 7.
-
Keep the same denominator: The denominator remains 4.
Therefore, 1 3/4 is equivalent to the improper fraction 7/4.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a simple yet powerful technique: multiplying by the reciprocal. The reciprocal of a fraction is obtained by swapping the numerator and the denominator.
For example, the reciprocal of 7/4 is 4/7.
To divide two fractions, follow these steps:
-
Convert any mixed numbers to improper fractions: As we've already done, 1 3/4 becomes 7/4.
-
Replace the division sign with a multiplication sign and use the reciprocal of the second fraction: Our problem becomes 4 ÷ (7/4), which transforms into 4 x (4/7).
-
Multiply the numerators together and the denominators together: Multiplying 4 (which can be written as 4/1) by 4/7 gives us (4 x 4) / (1 x 7) = 16/7.
-
Simplify the result (if possible): In this case, 16/7 is an improper fraction and can be converted back to a mixed number. To do this, divide the numerator (16) by the denominator (7). This gives us 2 with a remainder of 2. So, the simplified answer is 2 2/7.
Therefore, 4 divided by 1 3/4 is 2 2/7.
Let's solidify this with some practice problems:
Example 1: Solve 2/3 ÷ 1/2
-
No mixed numbers to convert.
-
Rewrite as 2/3 x 2/1 = 4/3
-
4/3 simplifies to 1 1/3.
Example 2: Solve 3 ÷ 2 1/5
-
Convert 2 1/5 to an improper fraction: (2 x 5 + 1)/5 = 11/5
-
Rewrite as 3/1 x 5/11 = 15/11
-
15/11 simplifies to 1 4/11.
Example 3: Solve 5 1/2 ÷ 3/4
-
Convert 5 1/2 to an improper fraction: (5 x 2 + 1)/2 = 11/2
-
Rewrite as 11/2 x 4/3 = 44/6
-
44/6 simplifies to 22/3, which is 7 1/3.
Advanced Concepts and Applications
Understanding fraction division extends beyond simple calculations. It's a fundamental skill in various fields:
-
Measurement and Scaling: Dividing fractions is crucial when working with measurements, such as dividing a length of wood into smaller pieces or scaling recipes in cooking.
-
Geometry and Area: Calculating areas of complex shapes often involves fraction division.
-
Algebra and Problem Solving: Many algebraic equations involve fraction manipulation and division.
-
Data Analysis: Analyzing data sets often involves calculating proportions and percentages, requiring fraction manipulation.
Troubleshooting Common Mistakes
Several common mistakes can occur when dividing fractions:
-
Forgetting to take the reciprocal: Remember, you must use the reciprocal of the second fraction before multiplying.
-
Incorrect conversion of mixed numbers: Double-check your work when converting mixed numbers to improper fractions.
-
Errors in multiplication: Carefully multiply numerators and denominators.
Conclusion
Dividing fractions, particularly those involving mixed numbers, might initially seem complex. However, by breaking down the problem into manageable steps – converting mixed numbers to improper fractions, using the reciprocal method, and simplifying the result – the process becomes straightforward. Mastering this skill is essential for success in mathematics and various applications across different fields. Consistent practice using diverse examples will solidify your understanding and build confidence in tackling more complex fraction problems. Remember to always double-check your work to avoid common mistakes and ensure accurate results.
Latest Posts
Latest Posts
-
Which Of These Phrases Is An Example Of Hyperbole
May 09, 2025
-
Write 4 1 2 As A Decimal Number
May 09, 2025
-
What Is 4 In Fraction Form
May 09, 2025
-
5 Is What Percent Of 100
May 09, 2025
-
Find The Exact Value Of Sin 105
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 1 3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.