What Is 1 3 Of 27
listenit
May 24, 2025 · 5 min read
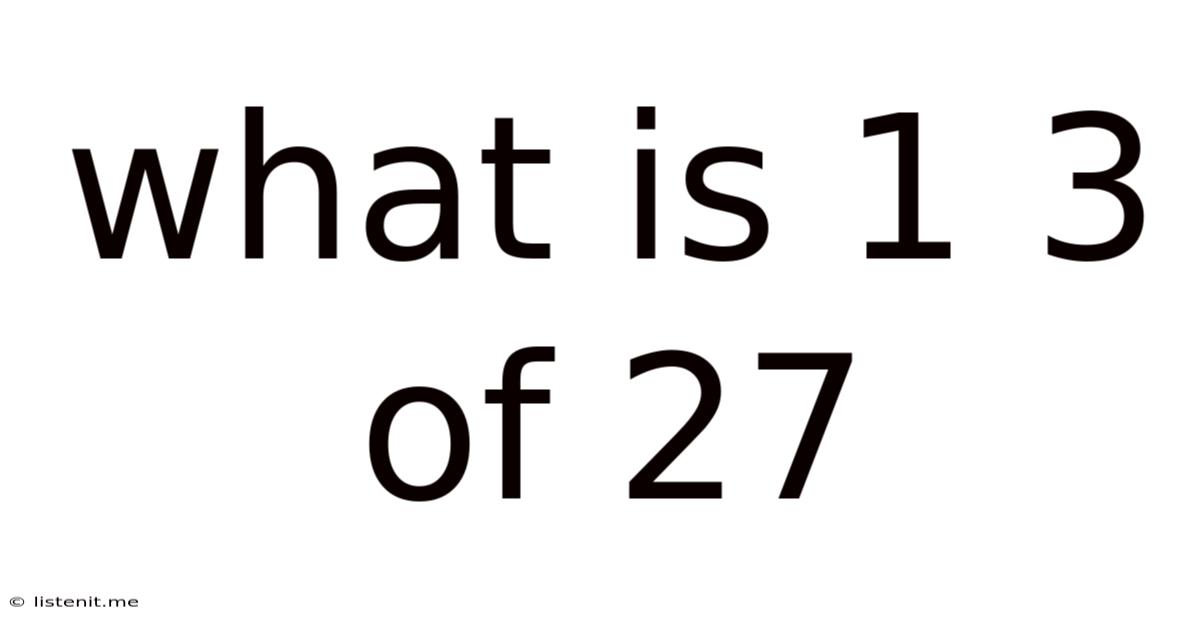
Table of Contents
What is 1/3 of 27? A Deep Dive into Fractions, Proportions, and Real-World Applications
The seemingly simple question, "What is 1/3 of 27?" opens the door to a fascinating exploration of fundamental mathematical concepts. While the answer itself is straightforward, understanding the underlying principles allows us to tackle more complex problems and appreciate the practical applications of fractions and proportions in various fields.
This article will not only provide the solution but delve into the meaning of fractions, explain different methods of solving this type of problem, explore real-world examples, and even touch upon advanced concepts related to fractions and their applications in higher mathematics.
Understanding Fractions: The Building Blocks of Proportion
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. In our case, 1/3 represents one part out of three equal parts.
Key Concepts Related to Fractions:
-
Equivalent Fractions: These are fractions that represent the same value, even though they look different. For instance, 1/3, 2/6, and 3/9 are all equivalent fractions. Understanding equivalent fractions is crucial for simplifying calculations and comparing fractions.
-
Simplifying Fractions: This involves reducing a fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, 6/9 can be simplified to 2/3 by dividing both by 3.
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to the denominator (e.g., 5/3). A mixed number combines a whole number and a proper fraction (e.g., 1 2/3). It's often easier to work with improper fractions when performing calculations.
-
Fraction Operations: Just like whole numbers, fractions can be added, subtracted, multiplied, and divided. Understanding these operations is essential for solving various mathematical problems.
Calculating 1/3 of 27: Three Different Approaches
There are several ways to calculate 1/3 of 27. Let's explore three common methods:
Method 1: Direct Multiplication
The most straightforward method involves directly multiplying the fraction by the whole number:
(1/3) * 27 = 27/3
This improper fraction can then be simplified by dividing the numerator (27) by the denominator (3):
27/3 = 9
Therefore, 1/3 of 27 is 9.
Method 2: Division
Since finding 1/3 of a number is equivalent to dividing the number by 3, we can directly divide 27 by 3:
27 ÷ 3 = 9
This method provides the same result, highlighting the relationship between fractions and division.
Method 3: Visual Representation
Imagine a group of 27 objects. To find 1/3 of 27, we would divide these 27 objects into three equal groups. Each group would contain:
27 ÷ 3 = 9 objects
This visual method helps solidify the concept of fractions and their relationship to division and partitioning.
Expanding the Understanding: Proportions and Ratios
The problem "What is 1/3 of 27?" can also be viewed as a proportion problem. A proportion is a statement that two ratios are equal. We can set up the proportion as follows:
1/3 = x/27
Where 'x' represents 1/3 of 27. To solve for 'x', we can cross-multiply:
1 * 27 = 3 * x
27 = 3x
Dividing both sides by 3, we get:
x = 9
This demonstrates the equivalence between fractions and proportions, providing another pathway to solve the problem.
Real-World Applications: From Baking to Budgeting
The concept of finding a fraction of a number is prevalent in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require specific fractions of ingredients. Knowing how to calculate 1/3 of a cup of flour or 1/2 of a teaspoon of baking powder is crucial for successful baking.
-
Budgeting and Finance: When planning a budget, we often need to allocate a certain fraction of our income to different expenses (e.g., 1/4 for rent, 1/5 for groceries).
-
Geometry and Measurement: Calculating areas and volumes often involves fractions. For example, finding the area of a triangle might require multiplying the base by the height and then dividing by 2 (which is equivalent to multiplying by 1/2).
-
Science and Engineering: Many scientific and engineering calculations involve fractions and proportions. For instance, calculating concentrations in chemistry or determining the ratio of components in a mixture.
-
Data Analysis and Statistics: Fractions and percentages are widely used in analyzing data and expressing proportions within datasets.
Beyond the Basics: Advanced Concepts and Applications
The fundamental understanding of fractions lays the groundwork for more advanced mathematical concepts:
-
Algebra: Solving algebraic equations often involves manipulating fractions and proportions.
-
Calculus: Calculus builds upon the foundations of algebra and analysis, requiring a deep understanding of fractions and limits.
-
Probability and Statistics: Probabilities are often expressed as fractions, and statistical analysis relies heavily on understanding proportions and ratios.
Conclusion: The Power of a Simple Fraction
The question "What is 1/3 of 27?" might seem elementary, but it serves as a powerful introduction to the world of fractions, proportions, and their pervasive applications in various fields. Mastering the concepts associated with fractions isn't just about solving mathematical problems; it's about developing a fundamental understanding of how to represent parts of a whole, understand ratios, and solve real-world problems involving proportions and quantities. By understanding these fundamental concepts, we unlock a broader understanding of mathematics and its application to everyday life. The seemingly simple answer, 9, represents much more than just a numerical value; it represents the culmination of a fundamental mathematical concept with far-reaching implications.
Latest Posts
Latest Posts
-
16 2 Is What Percent Of 45
May 24, 2025
-
Mean And Standard Deviation Of Sampling Distribution Calculator
May 24, 2025
-
What Is The Greatest Common Factor Of 8 And 32
May 24, 2025
-
What Time Will It Be In Nine Hours
May 24, 2025
-
10 Miles Per Second To Mph
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 3 Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.