What Is 1 2 X 3 4
listenit
May 24, 2025 · 5 min read
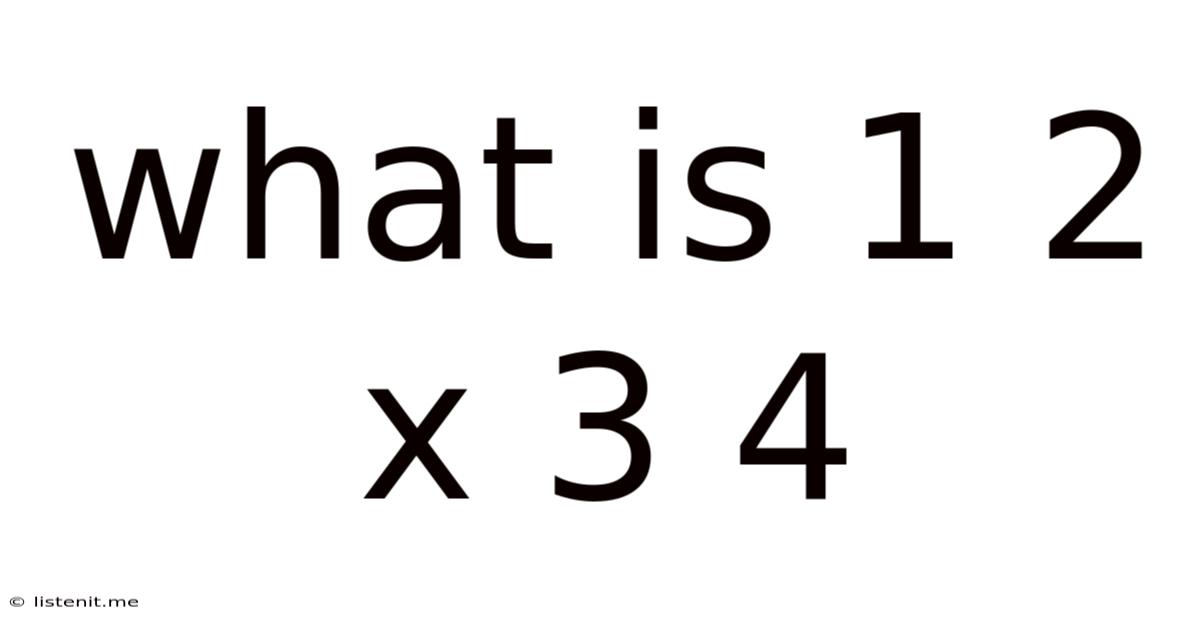
Table of Contents
What is 1 2 x 3 4? Unraveling the Mystery of Mathematical Notation
The seemingly simple expression "1 2 x 3 4" presents a fascinating challenge: its ambiguity. The lack of explicit operators between the numbers leaves room for multiple interpretations, highlighting the crucial role of clear mathematical notation. This article will explore the different ways we can interpret this expression, the resulting answers, and the broader implications for understanding mathematical language. We'll delve into the order of operations (PEMDAS/BODMAS), the importance of parentheses, and how seemingly minor details can significantly alter the outcome.
Understanding the Problem: Ambiguity in Mathematical Notation
The core issue lies in the absence of explicit operators. In standard mathematical notation, we use symbols like "+" (addition), "-" (subtraction), "×" or "*" (multiplication), and "÷" or "/" (division) to clearly indicate the operations to be performed. The expression "1 2 x 3 4" lacks these explicit symbols, leading to multiple valid interpretations depending on how we choose to insert them.
Possible Interpretations and Solutions
Let's explore some possible interpretations and their corresponding solutions:
1. Interpretation 1: Concatenation and Multiplication
One possible interpretation treats the numbers as being concatenated to form larger numbers before multiplication. This is a less common interpretation but perfectly valid within certain contexts.
- Process: We could interpret the expression as (12) x (34).
- Calculation: 12 × 34 = 408
- Result: 408
2. Interpretation 2: Implicit Multiplication and Addition/Subtraction
We can also assume implicit multiplication between adjacent numbers and then perform additional addition or subtraction operations. This interpretation requires inserting operators which are not explicitly stated.
- Process: One possibility is (1 + 2) × (3 + 4) = 3 x 7 = 21.
- Process: Another is (1 × 2) + (3 × 4) = 2 + 12 = 14.
- Process: Yet another is (1 × 2) × (3 × 4) = 2 × 12 = 24.
- Result: The results vary depending on the operators inserted.
3. Interpretation 3: Implicit Multiplication Only
Another interpretation assumes only implicit multiplication exists. In this case, the expression might be read as (1 × 2 × 3 × 4). This is a straight forward approach.
- Process: 1 × 2 × 3 × 4 = 24
- Result: 24
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), plays a critical role in resolving ambiguous expressions. However, even with PEMDAS/BODMAS, the ambiguity in "1 2 x 3 4" remains unless we add parentheses to clarify the intended operations.
PEMDAS/BODMAS and the Current Problem
The expression "1 2 x 3 4" does not inherently follow a specific order of operations because the operators themselves aren't defined. PEMDAS/BODMAS helps resolve expressions with a mixture of operators, but in the absence of explicitly stated operators, it's difficult to apply.
The Critical Role of Parentheses
Parentheses, or brackets, are essential tools for clarifying mathematical expressions. They explicitly define the order in which operations should be performed. Without them, ambiguities can arise, as demonstrated by our different interpretations of "1 2 x 3 4."
Illustrating the Impact of Parentheses
Let's see how parentheses remove ambiguity:
- (1 + 2) × (3 + 4): This clearly specifies that addition happens first within the parentheses, followed by the multiplication. The result is 21.
- (1 × 2) + (3 × 4): This shows that multiplication is performed within each parenthesis before the addition, resulting in 14.
- (1 × 2 × 3 × 4): This explicitly states that all multiplications should be performed sequentially, resulting in 24.
- 12 x 34: This eliminates ambiguity by concatenating the numbers before multiplication, resulting in 408.
Beyond the Numbers: Implications for Mathematical Communication
The ambiguity of "1 2 x 3 4" highlights a fundamental principle of mathematical communication: precision is paramount. Clear and unambiguous notation is crucial to avoid confusion and ensure that the intended meaning is accurately conveyed. This is vital not just for simple arithmetic problems but also for complex mathematical proofs and formulas. Poor notation can lead to errors, wasted time, and potentially incorrect conclusions.
Practical Applications and Real-world Scenarios
While the expression "1 2 x 3 4" might seem abstract, the principles it illustrates have significant practical applications:
- Programming: In programming languages, the order of operations is strictly defined, and parentheses are used to control the sequence of operations. Ambiguous expressions like "1 2 x 3 4" would likely result in a compiler error or unintended results.
- Engineering and Scientific Calculations: In engineering and scientific calculations, precision is absolutely critical. Ambiguous notation can have serious consequences, from minor inaccuracies to catastrophic failures. Proper use of parentheses and clear notation is essential to avoid these issues.
- Data Analysis and Statistics: Similar to programming and engineering, data analysis relies on precise mathematical operations. Any ambiguity can lead to incorrect analyses and misleading conclusions.
Conclusion: The Importance of Clear Mathematical Communication
The seemingly trivial expression "1 2 x 3 4" serves as a powerful reminder of the importance of clear and unambiguous mathematical notation. The lack of explicit operators demonstrates how easily misunderstandings can occur, leading to various interpretations and differing results. By understanding the role of order of operations, the power of parentheses, and the significance of precision in mathematical communication, we can avoid these pitfalls and ensure our mathematical work is accurate, efficient, and readily understood by others. Always prioritize clarity; when in doubt, use parentheses to eliminate any ambiguity and ensure your calculations are precisely what you intended.
Latest Posts
Latest Posts
-
What Is 4 Divided By 1 2
May 24, 2025
-
Cash On Cash Return Calculator Real Estate
May 24, 2025
-
If You Was Born In 1968 How Old Are You
May 24, 2025
-
15 Out Of 22 As A Percentage
May 24, 2025
-
Do I Have An Hourglass Shape
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 X 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.