What Is 1/2 Divided By 6 In Fraction Form
listenit
May 25, 2025 · 4 min read
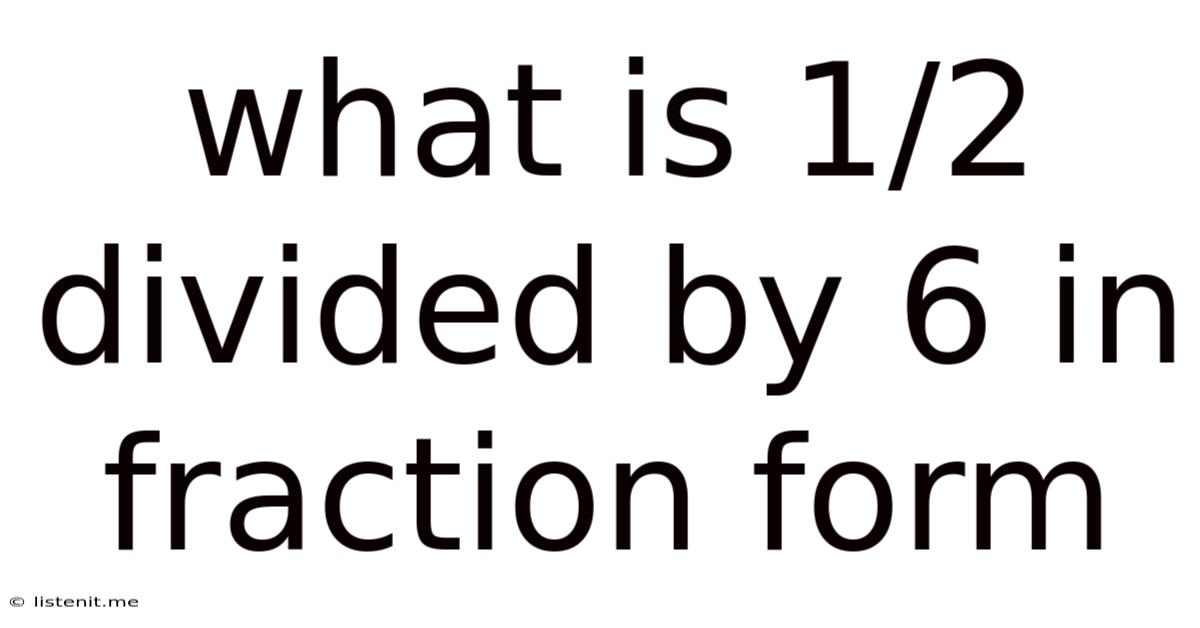
Table of Contents
What is 1/2 Divided by 6 in Fraction Form? A Comprehensive Guide
This comprehensive guide will delve into the seemingly simple problem of dividing the fraction 1/2 by the whole number 6. While the calculation itself is straightforward, understanding the underlying principles of fraction division is crucial for mastering more complex mathematical concepts. We'll not only solve the problem but also explore the various methods of solving fraction division problems, providing you with a solid foundation in this area of mathematics.
Understanding Fraction Division
Before tackling the specific problem of 1/2 divided by 6, let's establish a firm grasp on the fundamentals of dividing fractions. The core concept revolves around the idea of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. The reciprocal of a whole number is that number expressed as a fraction with 1 as the denominator. For example, the reciprocal of 6 is 1/6.
To divide a fraction by another fraction or a whole number, we follow these steps:
- Find the reciprocal of the divisor (the number you're dividing by).
- Change the division operation to multiplication.
- Multiply the first fraction by the reciprocal of the second fraction.
- Simplify the resulting fraction (if necessary).
Solving 1/2 Divided by 6
Now let's apply this knowledge to our problem: 1/2 divided by 6.
-
Find the reciprocal of 6: The reciprocal of 6 is 1/6.
-
Change the division to multiplication: Our problem now becomes 1/2 multiplied by 1/6.
-
Multiply the fractions: To multiply fractions, we multiply the numerators together and the denominators together:
(1/2) * (1/6) = (1 * 1) / (2 * 6) = 1/12
-
Simplify the fraction: In this case, the fraction 1/12 is already in its simplest form because 1 and 12 share no common factors other than 1.
Therefore, 1/2 divided by 6 is 1/12.
Alternative Methods and Visual Representations
While the reciprocal method is the most efficient, there are other ways to visualize and solve this problem. Let's explore a couple of them:
The "Keep, Change, Flip" Method
This mnemonic device helps remember the steps involved in fraction division:
- Keep: Keep the first fraction the same (1/2).
- Change: Change the division sign to a multiplication sign (×).
- Flip: Flip the second fraction (6 becomes 1/6).
This leads to the same calculation: (1/2) × (1/6) = 1/12.
Visual Representation using Area Models
Imagine a rectangle representing 1 whole unit. Dividing this rectangle in half gives you a representation of 1/2. Now, if you divide that half into 6 equal parts, each part represents 1/12 of the whole rectangle. This visual approach provides an intuitive understanding of the result.
Expanding on Fraction Division: More Complex Examples
Let's solidify your understanding with some more complex examples, building upon the principles we've covered:
Example 1: 2/3 divided by 4/5
-
Find the reciprocal of 4/5: The reciprocal is 5/4.
-
Change to multiplication: (2/3) × (5/4)
-
Multiply: (2 × 5) / (3 × 4) = 10/12
-
Simplify: 10/12 simplifies to 5/6 (both numerator and denominator are divisible by 2).
Therefore, 2/3 divided by 4/5 is 5/6.
Example 2: 3 divided by 1/4
-
Find the reciprocal of 1/4: The reciprocal is 4/1 or simply 4.
-
Change to multiplication: 3 × 4
-
Multiply: 3 × 4 = 12
Therefore, 3 divided by 1/4 is 12.
Example 3: 5/8 divided by 15/16
-
Find the reciprocal of 15/16: The reciprocal is 16/15.
-
Change to multiplication: (5/8) × (16/15)
-
Multiply: (5 × 16) / (8 × 15) = 80/120
-
Simplify: 80/120 simplifies to 2/3 (both numerator and denominator are divisible by 40).
Therefore, 5/8 divided by 15/16 is 2/3.
Practical Applications of Fraction Division
Understanding fraction division isn't just about solving textbook problems; it has practical applications in various real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions to adjust ingredient amounts.
- Sewing and Crafting: Calculating fabric needs or dividing materials for projects often involves fraction division.
- Construction and Engineering: Precise measurements and material calculations often require working with fractions.
- Data Analysis: Representing and interpreting data often uses fractions and requires division to understand proportions.
Conclusion: Mastering Fraction Division for Enhanced Mathematical Proficiency
Mastering fraction division is a cornerstone of mathematical proficiency. By understanding the concept of reciprocals and applying the steps outlined in this guide, you'll be able to confidently tackle a wide range of fraction division problems. Remember to practice regularly, using both the standard method and alternative approaches like visual representations, to reinforce your understanding. This will not only improve your mathematical skills but also enhance your problem-solving abilities in various real-world applications. The seemingly simple problem of 1/2 divided by 6 serves as an excellent starting point for building a strong foundation in this important area of mathematics. From there, you can progress to more complex calculations with confidence and ease. Keep practicing, and you'll find that fraction division becomes second nature.
Latest Posts
Latest Posts
-
What Is The Gcf Of 50 And 20
May 25, 2025
-
20 Out Of 30 Is What Percent
May 25, 2025
-
How Many Btus Needed Per Square Foot
May 25, 2025
-
What Is The Gcf Of 56 And 40
May 25, 2025
-
11 Out Of 23 As A Percentage
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 Divided By 6 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.