Solve For X In The Equation X 2 17
listenit
May 09, 2025 · 5 min read
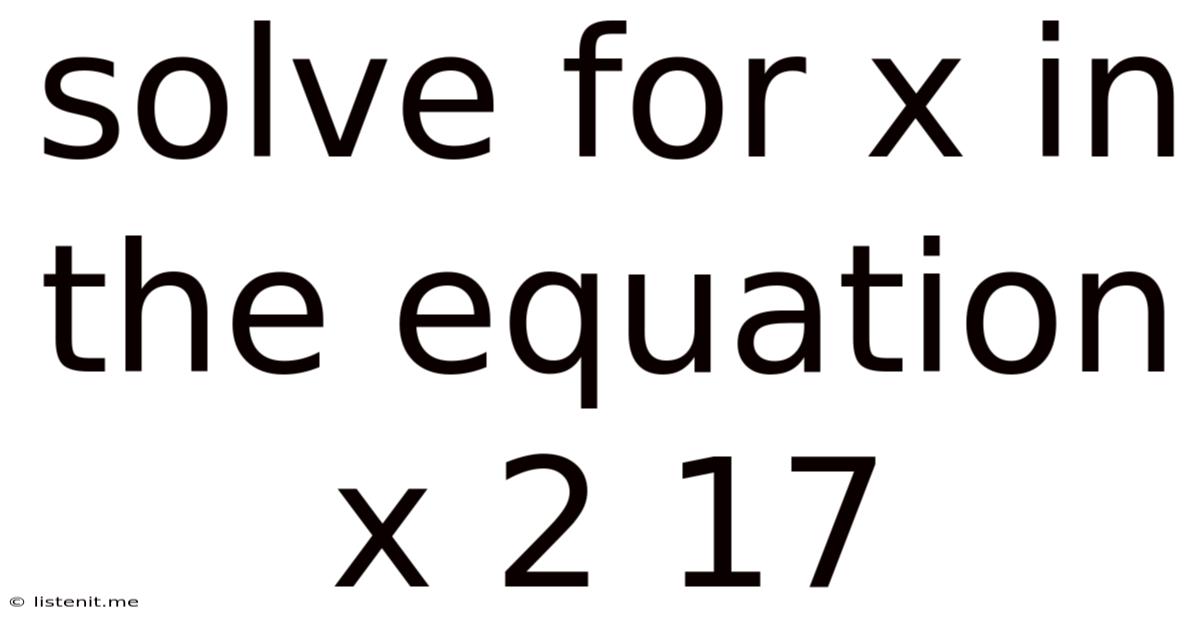
Table of Contents
Solving for x in the Equation x² = 17: A Comprehensive Guide
The seemingly simple equation, x² = 17, presents a valuable opportunity to explore fundamental algebraic concepts and delve into the intricacies of solving quadratic equations. While the solution might appear straightforward at first glance, understanding the underlying principles and exploring different approaches will solidify your understanding of algebra and its applications. This comprehensive guide will walk you through various methods to solve for 'x', explaining the rationale behind each step and highlighting potential pitfalls to avoid.
Understanding the Problem: What Does x² = 17 Mean?
Before we jump into the solutions, let's clarify what the equation x² = 17 is asking us to find. The equation states that when a number ('x') is multiplied by itself, the result is 17. This implies that 'x' is the square root of 17. However, remember that squaring both positive and negative numbers results in a positive value. Therefore, we anticipate two solutions for 'x'.
Method 1: The Square Root Method – The Most Direct Approach
The most direct method to solve for 'x' in x² = 17 is to take the square root of both sides of the equation. This is a fundamental algebraic operation that maintains the equality of the equation as long as we apply it consistently to both sides.
Steps:
-
Start with the equation: x² = 17
-
Take the square root of both sides: √x² = ±√17 (Note the ± symbol. This is crucial because both positive and negative square roots of 17 will satisfy the equation).
-
Simplify: x = ±√17
Therefore, the solutions are x = √17 and x = -√17. These are the exact solutions. We can approximate these values using a calculator:
- x ≈ 4.123
- x ≈ -4.123
Method 2: Factoring – A Less Direct, but Equally Valid Approach
While less straightforward for this particular equation, factoring is a crucial technique for solving more complex quadratic equations. In this case, we can rewrite the equation as a difference of squares, although it requires a bit of manipulation.
Steps:
-
Rewrite the equation: x² - 17 = 0
-
Recognize it's not easily factorable: 17 is a prime number, meaning it has no integer factors other than 1 and itself. This makes direct factoring challenging. However, we can still conceptually approach it as a difference of squares.
-
Express as a difference of squares (conceptually): We can think of this as x² - (√17)² = 0. This form resembles a difference of squares, a² - b² = (a + b)(a - b).
-
Factor (conceptually): (x - √17)(x + √17) = 0
-
Solve for x: Setting each factor to zero gives us x = √17 and x = -√17.
This method showcases the conceptual link between factoring and square roots in solving quadratic equations, even when direct factoring isn't immediately apparent.
Method 3: Quadratic Formula – The Universal Solver
The quadratic formula is a powerful tool that can solve any quadratic equation of the form ax² + bx + c = 0. Our equation, x² = 17, can be rewritten in this form as x² + 0x - 17 = 0, where a = 1, b = 0, and c = -17.
Steps:
-
Identify a, b, and c: a = 1, b = 0, c = -17
-
Apply the quadratic formula: x = [-b ± √(b² - 4ac)] / 2a
-
Substitute the values: x = [0 ± √(0² - 4 * 1 * -17)] / (2 * 1)
-
Simplify: x = ±√68 / 2
-
Further simplification: √68 = √(4 * 17) = 2√17
-
Final Solution: x = ±2√17 / 2 = ±√17
Again, we arrive at the same solutions: x = √17 and x = -√17. The quadratic formula demonstrates its versatility in solving quadratic equations, regardless of their specific form.
Understanding the Solutions and Their Significance
The solutions x = √17 and x = -√17 represent the two points on the number line whose squares equal 17. Graphically, this can be visualized as the intersection points of the parabola y = x² and the horizontal line y = 17.
The approximate values (x ≈ 4.123 and x ≈ -4.123) provide a numerical representation of these points. However, it's important to remember that √17 and -√17 are the exact solutions, while the decimal approximations are only approximations with inherent rounding errors.
Expanding the Concept: Solving More Complex Quadratic Equations
The principles applied to solving x² = 17 can be extended to solve more complex quadratic equations. Understanding the different methods – the square root method, factoring, and the quadratic formula – provides a robust toolkit for tackling a wide range of quadratic equations. The key is to identify the most efficient method based on the specific characteristics of the equation.
For instance, equations like x² - 5x + 6 = 0 can be easily factored, while equations like 2x² + 3x - 7 = 0 might require the quadratic formula for a precise solution. The ability to choose the appropriate method enhances problem-solving efficiency and accuracy.
Practical Applications: Where Do Quadratic Equations Appear in Real Life?
Quadratic equations are not merely abstract mathematical concepts; they have numerous applications in various fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
- Engineering: Designing structures, analyzing stresses and strains in materials.
- Economics: Modeling market trends, predicting economic growth or decline.
- Computer Graphics: Creating curves and shapes for 2D and 3D graphics.
Conclusion: Mastering the Fundamentals of Quadratic Equations
Solving for x in the equation x² = 17 is a foundational step in understanding quadratic equations. Mastering various solution methods like the square root method, factoring, and the quadratic formula equips you with the tools to tackle more complex problems. Remember that understanding the underlying principles – like the concept of square roots and the importance of considering both positive and negative solutions – is crucial for success in algebra and its applications in numerous real-world scenarios. This comprehensive guide serves as a starting point for your journey into the fascinating world of quadratic equations and their multifaceted applications.
Latest Posts
Latest Posts
-
When To Use Direct Comparison Vs Limit Comparison
May 09, 2025
-
What Is The Fraction Of 0 02
May 09, 2025
-
What Is The Decimal Of 1 20
May 09, 2025
-
Convert 350 Degrees F To Celsius
May 09, 2025
-
How Could You Test For Hydrogen Gas
May 09, 2025
Related Post
Thank you for visiting our website which covers about Solve For X In The Equation X 2 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.