What Is The Decimal Of 1/20
listenit
May 09, 2025 · 5 min read
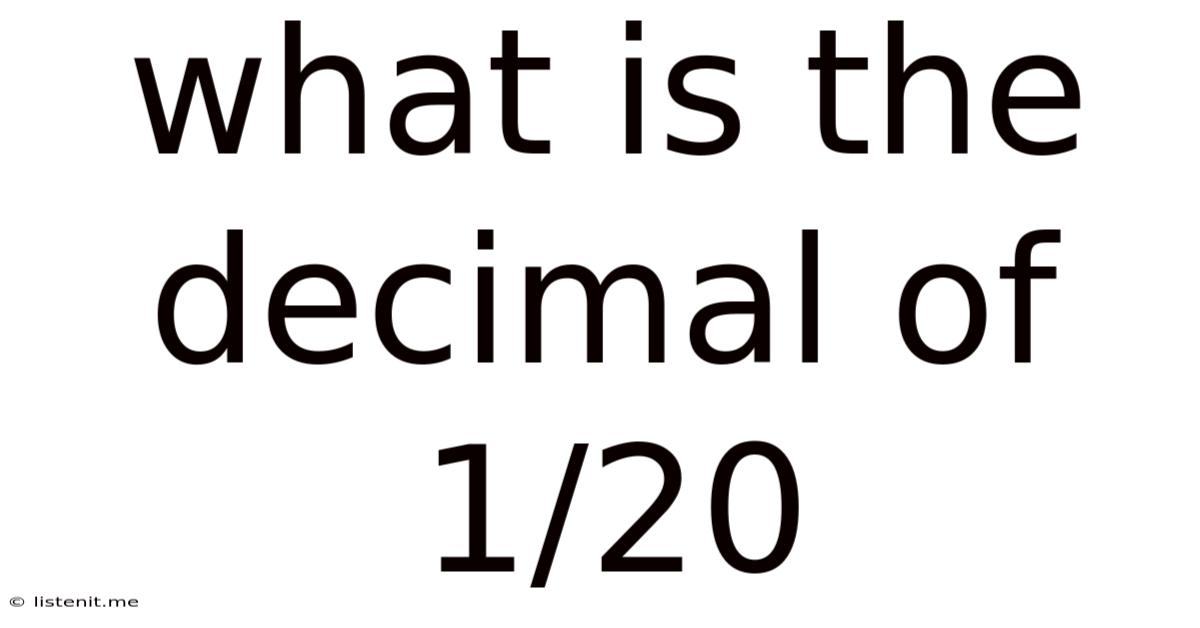
Table of Contents
What is the Decimal of 1/20? A Deep Dive into Fraction-to-Decimal Conversion
The seemingly simple question, "What is the decimal of 1/20?" opens a door to a fascinating world of mathematical concepts and practical applications. While the answer itself is straightforward, exploring the how and why behind the conversion provides valuable insights into fractions, decimals, and their interconnectedness. This comprehensive guide delves into the process, explores related concepts, and showcases the relevance of this seemingly basic conversion in various fields.
Understanding Fractions and Decimals
Before diving into the specifics of converting 1/20 to a decimal, let's establish a clear understanding of fractions and decimals themselves.
Fractions: Representing Parts of a Whole
Fractions represent parts of a whole. They are expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For instance, in the fraction 1/20, 1 represents the part we're considering, and 20 represents the total number of equal parts the whole is divided into.
Decimals: Another Way to Represent Parts of a Whole
Decimals are another way to represent parts of a whole. They use a base-ten system, where each digit to the right of the decimal point represents a power of ten (tenths, hundredths, thousandths, and so on). For example, 0.5 represents five-tenths, and 0.25 represents twenty-five hundredths.
Converting 1/20 to a Decimal: The Methods
There are several ways to convert the fraction 1/20 to its decimal equivalent. Let's explore the most common methods:
Method 1: Direct Division
The most fundamental method is through direct division. We divide the numerator (1) by the denominator (20):
1 ÷ 20 = 0.05
This method directly translates the fractional representation into its decimal equivalent. The result, 0.05, signifies five hundredths.
Method 2: Equivalent Fractions and Decimal Representation
We can convert 1/20 into an equivalent fraction with a denominator that is a power of 10. This makes the conversion to a decimal simpler. Since 20 is a factor of 100 (20 x 5 = 100), we can multiply both the numerator and denominator by 5:
(1 x 5) / (20 x 5) = 5/100
Now, the fraction 5/100 can be easily written as a decimal:
5/100 = 0.05
This method highlights the equivalence between fractions and showcases how manipulating the fraction can simplify the conversion.
Method 3: Using a Calculator
While not inherently a mathematical method, using a calculator provides a quick and efficient way to obtain the decimal equivalent. Simply enter 1 ÷ 20 and the calculator will display 0.05. This method is particularly useful for more complex fractions.
The Significance of 0.05: Applications and Context
The decimal 0.05, the equivalent of 1/20, has various applications across different fields. Understanding its significance in different contexts is crucial.
Finance and Percentages
In finance, 0.05 often represents 5% (five percent). This is because percentages are simply fractions with a denominator of 100. Therefore, 0.05 is frequently used in calculating interest rates, discounts, tax rates, and other financial computations. For example, a 5% discount on a $100 item would be calculated as 0.05 x $100 = $5.
Measurement and Engineering
In measurement and engineering, 0.05 can represent units of measurement. For instance, it could represent 0.05 meters, 0.05 kilograms, or 0.05 seconds, depending on the context. Precision in measurements often requires working with decimals, making this conversion highly relevant in these fields.
Statistics and Probability
In statistics and probability, 0.05 is often used as a significance level (p-value). It's a threshold used to determine the statistical significance of results. A p-value of 0.05, or less, often suggests that the observed results are unlikely to have occurred by chance.
Programming and Computer Science
In programming and computer science, understanding decimal representation is crucial. Many programming languages use floating-point numbers to represent decimals. The conversion of fractions to decimals is fundamental for performing calculations involving fractional values.
Beyond 1/20: Generalizing Fraction-to-Decimal Conversion
The principles used to convert 1/20 to a decimal are applicable to other fractions. The process generally involves dividing the numerator by the denominator. However, some fractions yield terminating decimals (like 1/20), while others yield repeating decimals (like 1/3).
Terminating Decimals: Fractions with Denominators that are Powers of 2 and/or 5
Fractions whose denominators can be expressed as powers of 2 and/or 5 (or a combination thereof) will always result in terminating decimals. This is because these denominators can always be converted into a power of 10, simplifying the conversion to a decimal.
Repeating Decimals: Fractions with Denominators that are Not Powers of 2 and/or 5
Fractions with denominators that cannot be expressed solely as powers of 2 and/or 5 often result in repeating decimals. These decimals have a sequence of digits that repeat infinitely. For example, 1/3 = 0.3333... (the digit 3 repeats infinitely).
Practical Applications and Real-World Examples
The ability to convert fractions to decimals has numerous real-world applications. Here are a few examples:
- Calculating discounts: As mentioned earlier, understanding decimal equivalents is crucial for calculating percentage discounts.
- Baking and cooking: Recipes often involve fractional measurements (e.g., 1/2 cup of sugar). Converting these fractions to decimals can improve precision and accuracy.
- Construction and design: Accurate measurements are critical in construction and design, often involving fractional values that need to be converted to decimals for precise calculations.
- Financial analysis: Many financial calculations involve percentages and fractional values, highlighting the importance of understanding decimal conversions.
- Scientific research: Scientific measurements often involve fractional values that need conversion for data analysis and interpretation.
Conclusion: The Importance of Mastering Fraction-to-Decimal Conversion
The seemingly simple conversion of 1/20 to 0.05 underscores the fundamental interconnectedness of fractions and decimals. Mastering this conversion is not just about solving a mathematical problem; it's about gaining a deeper understanding of mathematical concepts and their application in diverse fields. From finance and engineering to programming and scientific research, the ability to seamlessly navigate between fractional and decimal representations is a valuable skill with far-reaching implications. The next time you encounter a fraction, remember the simple yet powerful process of conversion, and appreciate its wide-ranging significance in our quantitative world.
Latest Posts
Latest Posts
-
The Rate Of Reaction Depends On
May 10, 2025
-
What Is The Value Of 12 0
May 10, 2025
-
210 At 8 For 7 Years
May 10, 2025
-
How To Find C In Standard Form
May 10, 2025
-
Definition Of Turning Point In Math
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal Of 1/20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.