Sin X 2 Cos X 2
listenit
Mar 27, 2025 · 6 min read
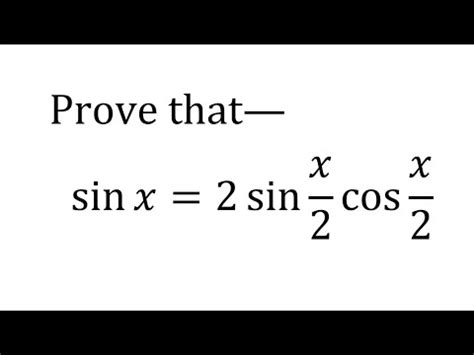
Table of Contents
Exploring the Trigonometric Identity: sin x / 2 cos x / 2
The expression sin x / 2 cos x / 2 forms a foundational element within trigonometry, offering a gateway to understanding more complex identities and their applications in various fields like physics, engineering, and computer graphics. While seemingly simple, this expression holds significant mathematical weight and provides opportunities for insightful exploration. This article delves deep into the intricacies of sin x / 2 cos x / 2, exploring its transformations, derivations, and practical applications. We'll analyze its relationship to other trigonometric functions, discuss its graphical representation, and highlight its significance in solving real-world problems.
Understanding the Core: Double Angle Identities
Before embarking on a detailed analysis of sin x / 2 cos x / 2, it's crucial to establish a strong understanding of the double angle identities. These identities form the backbone of many trigonometric manipulations and are essential for simplifying complex expressions.
The double angle identities for sine and cosine are:
- sin 2x = 2 sin x cos x
- cos 2x = cos²x - sin²x = 1 - 2sin²x = 2cos²x - 1
These identities allow us to express trigonometric functions of double angles (2x) in terms of functions of single angles (x). This relationship proves invaluable when simplifying or transforming expressions involving both single and double angles.
Transforming sin x / 2 cos x / 2: A Step-by-Step Approach
The expression sin x / 2 cos x / 2 itself isn't directly represented in the standard double angle identities. However, we can manipulate it using the double angle formula for sine. Let's consider the following:
Let y = x / 2. Then x = 2y. Substituting this into our expression, we get:
sin y cos y
Now, recall the double angle identity for sine: sin 2y = 2 sin y cos y. Therefore, we can rewrite sin y cos y as:
sin y cos y = (1/2) sin 2y
Substituting back x / 2 for y, we arrive at:
sin x / 2 cos x / 2 = (1/2) sin x
This transformation reveals a crucial connection: the expression sin x / 2 cos x / 2 is simply half the sine of the original angle x. This simplification makes it easier to work with in various contexts.
Graphical Representation and Analysis
Visualizing the function helps solidify our understanding. Let's consider the graphs of sin x and (1/2)sin x. The graph of (1/2)sin x is a scaled-down version of sin x, with its amplitude reduced to 1/2. This means the maximum value is 1/2 and the minimum value is -1/2, while maintaining the same period as sin x (2π).
This graphical representation clearly illustrates the relationship between sin x / 2 cos x / 2 and sin x. The former is always half the value of the latter for any given x. Understanding this visual connection reinforces the mathematical derivation.
Applications in Calculus and Differential Equations
The simplified form (1/2)sin x makes sin x / 2 cos x / 2 particularly convenient for calculus operations. Finding derivatives and integrals becomes significantly simpler.
Differentiation:
The derivative of (1/2)sin x is (1/2)cos x. This straightforward result highlights the ease of handling the transformed expression.
Integration:
Similarly, the integral of (1/2)sin x is -(1/2)cos x + C (where C is the constant of integration). This simple integration is a direct consequence of the expression's transformation.
Applications in Physics and Engineering
Trigonometric functions, including variations like sin x / 2 cos x / 2, are ubiquitous in physics and engineering. They often model oscillatory or wave-like phenomena.
Simple Harmonic Motion (SHM): SHM describes the motion of a pendulum or a mass on a spring. The displacement, velocity, and acceleration can be represented using sine and cosine functions. The simplified form of our expression could simplify calculations involving such systems.
Wave Phenomena: Waves, whether sound waves, light waves, or water waves, often have sinusoidal characteristics. The ability to easily manipulate expressions like sin x / 2 cos x / 2 can greatly simplify analysis and calculations related to wave propagation, interference, and diffraction.
Applications in Computer Graphics and Game Development
In computer graphics and game development, trigonometric functions are frequently used for tasks such as:
- Rotation: Rotating objects in 2D or 3D space involves using sine and cosine functions to calculate new coordinates. Simplifying trigonometric expressions can improve computational efficiency, leading to smoother animations and faster rendering.
- Animation: Creating realistic and fluid animations often relies on trigonometric functions to model movement and changes in object properties.
- Lighting and Shading: Calculating the illumination of surfaces often involves intricate trigonometric calculations, where simplifying expressions like ours can improve performance.
Solving Trigonometric Equations: An Illustrative Example
Let's illustrate the practical application of our transformed expression by solving a trigonometric equation. Consider the equation:
sin x / 2 cos x / 2 = 1/4
Using our transformation, we can rewrite the equation as:
(1/2)sin x = 1/4
Multiplying both sides by 2, we get:
sin x = 1/2
This is a standard trigonometric equation. The solutions are:
x = π/6 + 2kπ and x = 5π/6 + 2kπ (where k is an integer)
This example demonstrates how transforming the original expression simplifies the process of solving trigonometric equations, making it more manageable and efficient.
Advanced Considerations: Product-to-Sum Formulas and Beyond
While we've focused primarily on the double angle formula, the expression sin x / 2 cos x / 2 can also be explored using product-to-sum formulas. These formulas provide alternative ways to express products of trigonometric functions as sums or differences of trigonometric functions.
Applying product-to-sum formulas might offer alternative solutions or perspectives when dealing with more complex scenarios involving sin x / 2 cos x / 2 within larger equations or expressions. This exploration reveals the interconnectedness of various trigonometric identities and underscores the power of choosing the most efficient approach based on the specific problem.
Conclusion: The Significance of sin x / 2 cos x / 2
The seemingly simple expression sin x / 2 cos x / 2, once transformed into its equivalent (1/2)sin x, reveals its significant role in trigonometry and its applications. Its simplified form facilitates easier calculations in calculus, allows for straightforward solutions to trigonometric equations, and offers valuable efficiency in physics, engineering, and computer graphics. Understanding this expression and its relationships to other trigonometric identities strengthens one's overall comprehension of this fundamental area of mathematics. Further exploration of its interactions with product-to-sum formulas and other advanced trigonometric techniques opens doors to even more complex and rewarding mathematical insights. This exploration demonstrates the far-reaching impact of a seemingly simple trigonometric expression and its significance across multiple scientific and computational domains.
Latest Posts
Latest Posts
-
What Is The Oxidation Number Of Sodium
Mar 30, 2025
-
Cuanto Es 168 Cm En Pies
Mar 30, 2025
-
How Many Radians In One Revolution
Mar 30, 2025
-
What Is 16666 As A Fraction
Mar 30, 2025
-
What Color Are The Coolest Stars
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Sin X 2 Cos X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
