Simplify The Square Root Of 34
listenit
Mar 29, 2025 · 5 min read
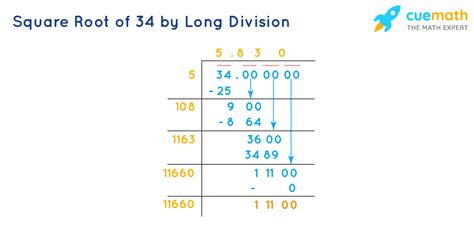
Table of Contents
Simplifying the Square Root of 34: A Comprehensive Guide
Simplifying square roots is a fundamental concept in mathematics, crucial for various applications ranging from basic algebra to advanced calculus. While some square roots simplify neatly into whole numbers (e.g., √16 = 4), others, like √34, require a more methodical approach. This article provides a comprehensive guide to simplifying √34, exploring the underlying principles and demonstrating different methods. We'll delve into the concept of prime factorization, perfect squares, and how to express the simplified form in its most efficient representation. Beyond √34, we'll also examine how these principles extend to simplifying other square roots, empowering you with a versatile skill set for tackling various mathematical problems.
Understanding Square Roots and Simplification
Before diving into the simplification of √34, let's establish a foundational understanding of square roots and the process of simplification. A square root is a number that, when multiplied by itself, produces a given number. For instance, the square root of 9 (√9) is 3 because 3 x 3 = 9.
Simplifying a square root involves expressing it in its most efficient form. This often involves extracting any perfect square factors from the radicand (the number under the square root symbol). A perfect square is a number that results from squaring a whole number (e.g., 4, 9, 16, 25, etc.).
The core principle behind simplifying square roots lies in the property √(a x b) = √a x √b. This property allows us to break down a complex square root into simpler components.
Prime Factorization: The Key to Simplification
The most effective method for simplifying square roots, particularly those of larger numbers like 34, is through prime factorization. Prime factorization involves expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that have only two divisors: 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's apply prime factorization to 34:
34 = 2 x 17
Both 2 and 17 are prime numbers, meaning we've reached the end of the factorization. Notice that neither 2 nor 17 are perfect squares. This indicates that √34 cannot be simplified further into a whole number or a simpler radical expression containing only whole numbers within the square root symbol.
Simplifying √34: The Final Result
Since the prime factorization of 34 reveals no perfect square factors, the simplest form of √34 remains √34. There's no way to extract a whole number from the square root without introducing an approximation. This is because neither 2 nor 17 are perfect squares, hence, simplifying involves no further actions beyond confirming the absence of perfect square factors. This is a perfectly valid and often the simplest and most precise representation.
Approximating √34: Exploring Decimal Values
While √34 cannot be simplified further into a radical expression containing only whole numbers within the square root symbol, we can approximate its decimal value. Using a calculator, we find that √34 ≈ 5.83. However, it's important to remember that this is an approximation, not an exact representation. The exact value remains √34.
Extending the Principles: Simplifying Other Square Roots
The principles we used to simplify √34 apply equally to other square roots. Let's consider a few examples:
Example 1: Simplifying √72
- Prime Factorization: 72 = 2 x 2 x 2 x 3 x 3 = 2² x 3² x 2
- Identifying Perfect Squares: We have 2² and 3²
- Simplification: √72 = √(2² x 3² x 2) = √2² x √3² x √2 = 2 x 3 x √2 = 6√2
Therefore, √72 simplifies to 6√2.
Example 2: Simplifying √128
- Prime Factorization: 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2⁷
- Identifying Perfect Squares: We can express this as 2⁶ x 2 = (2³)² x 2
- Simplification: √128 = √((2³)² x 2) = √(2³)² x √2 = 8√2
Therefore, √128 simplifies to 8√2.
Example 3: Simplifying √147
- Prime Factorization: 147 = 3 x 7 x 7 = 3 x 7²
- Identifying Perfect Squares: We have 7²
- Simplification: √147 = √(3 x 7²) = √3 x √7² = 7√3
Therefore, √147 simplifies to 7√3.
These examples illustrate the power of prime factorization in simplifying square roots. By consistently applying this method, you can efficiently simplify a wide range of square roots, regardless of their complexity.
Practical Applications of Simplifying Square Roots
Simplifying square roots isn't merely an abstract mathematical exercise; it holds practical applications across various fields:
- Geometry: Calculating distances, areas, and volumes often involves square roots. Simplifying these roots ensures accuracy and efficiency in calculations.
- Physics: Many physical formulas, especially those related to motion, energy, and forces, involve square roots. Simplifying these roots is crucial for solving problems effectively.
- Engineering: Structural analysis, electrical engineering, and numerous other engineering disciplines rely heavily on mathematical calculations involving square roots.
- Computer Graphics: The rendering of 3D graphics frequently uses calculations involving square roots. Efficient simplification contributes to faster and smoother rendering.
Conclusion: Mastering the Art of Simplification
Simplifying square roots, as demonstrated through the detailed analysis of √34 and the examples provided, is a fundamental skill in mathematics with wide-ranging applications. By understanding prime factorization and the properties of perfect squares, you can confidently tackle even complex square root simplifications. Remember that while some square roots, like √34, cannot be simplified beyond their basic form, the process of attempting simplification helps you arrive at the most precise and efficient representation. The ability to seamlessly simplify square roots is a testament to your mathematical proficiency and will undoubtedly prove valuable in many mathematical and real-world contexts.
Latest Posts
Latest Posts
-
Are Liquids Included In Equilibrium Constant
Apr 01, 2025
-
1 1 2 As An Improper Fraction
Apr 01, 2025
-
How To Find The X Intercepts Of A Parabola
Apr 01, 2025
-
What Is 1 9 As A Decimal
Apr 01, 2025
-
What Is The Inverse Of 3 X
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 34 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
