Seven Times The Difference Of A Number And 7.
listenit
May 10, 2025 · 5 min read
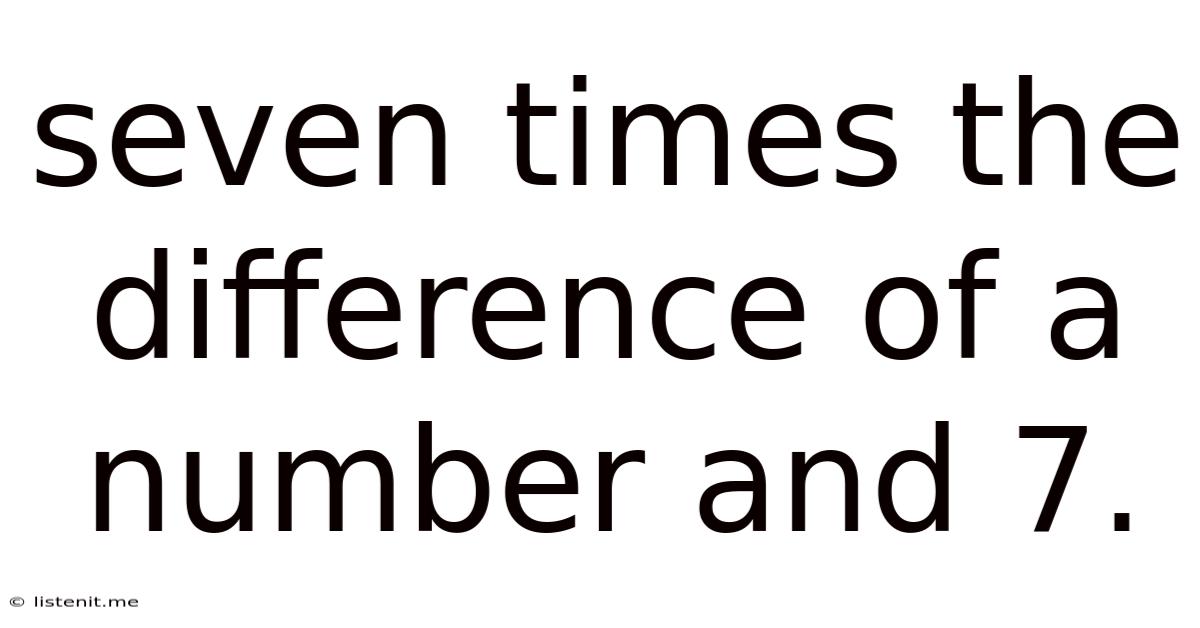
Table of Contents
Seven Times the Difference of a Number and 7: A Deep Dive into Mathematical Expressions
This article delves into the mathematical expression "seven times the difference of a number and 7," exploring its various interpretations, applications, and the underlying algebraic principles involved. We'll unpack the expression, examine how to translate it into mathematical notation, solve related equations, and discuss its practical applications. We'll also consider potential extensions and variations of the expression to broaden our understanding.
Understanding the Expression: Deconstructing the Language
The phrase "seven times the difference of a number and 7" might seem simple at first glance, but understanding its components is crucial for accurate mathematical representation. Let's break it down:
- A number: This represents an unknown value, typically denoted by a variable like x, y, or n.
- The difference of a number and 7: This indicates subtraction; we're finding the result of subtracting 7 from our unknown number. Mathematically, this is written as x - 7 (assuming we use x as our variable).
- Seven times: This signifies multiplication by 7.
Therefore, the entire expression translates to 7 multiplied by the difference of a number and 7.
Translating into Mathematical Notation: From Words to Symbols
The power of mathematics lies in its ability to concisely represent complex ideas using symbols. Let's convert our phrase into a clear mathematical expression:
7(x - 7)
This concise notation perfectly captures the meaning of the original phrase. The parentheses are essential; they indicate that the subtraction operation (x - 7) must be performed before the multiplication by 7. Without the parentheses, the expression would be interpreted differently, leading to an incorrect result.
Solving Equations Involving the Expression
Now, let's explore how this expression can be used in equations. Suppose we have an equation like this:
7(x - 7) = 28
This equation states that "seven times the difference of a number and 7 is equal to 28." To solve for x, we follow these steps:
-
Distribute the 7: Multiply 7 by both terms inside the parentheses: 7x - 49 = 28
-
Add 49 to both sides: This isolates the term with x: 7x = 77
-
Divide both sides by 7: This solves for x: x = 11
Therefore, the number x is 11. We can check our answer by substituting it back into the original equation: 7(11 - 7) = 7(4) = 28. The equation holds true.
Let's consider a slightly more complex scenario:
7(x - 7) + 14 = 42
-
Subtract 14 from both sides: 7(x - 7) = 28
-
Now we're back to our previous equation: Following the steps above, we again find that x = 11.
These examples demonstrate how to manipulate equations containing our expression to find the unknown value. The key is to carefully apply the order of operations (PEMDAS/BODMAS) and perform inverse operations to isolate the variable.
Applications and Real-World Examples
While this expression might seem purely abstract, it has practical applications in various real-world scenarios. Consider these examples:
-
Discounts and Sales: Imagine a store offering a 70% discount (7 times 10%) on items priced $7 above a certain base price. If the base price is represented by x, the final price after the discount could be modeled using a variation of our expression.
-
Profit Margins: A business might calculate its profit by taking seven times the difference between its revenue and production costs.
-
Temperature Conversions: While not a direct application, the principles of manipulating expressions involving multiplication and subtraction are fundamental to various conversions and formulas in physics and engineering.
-
Geometry: Problems involving area calculations or perimeter calculations of certain shapes might involve expressions similar to the one we're studying.
Extensions and Variations: Expanding the Scope
We can extend our understanding by considering variations of the expression:
-
Changing the multiplier: Instead of 7, we could use any other number. For example, "five times the difference of a number and 7" would be written as 5(x - 7).
-
Changing the subtracted number: We could change the number being subtracted. "Seven times the difference of a number and 5" would be written as 7(x - 5).
-
Introducing additional operations: We could add or subtract other numbers to the expression, creating more complex equations. For example: 7(x - 7) + 10 = 54
Inequalities and the Expression
Instead of equations, we can also work with inequalities:
7(x - 7) > 28
This inequality states that "seven times the difference of a number and 7 is greater than 28." Solving this requires similar steps to solving equations, but the solution will be a range of values rather than a single number.
-
Distribute the 7: 7x - 49 > 28
-
Add 49 to both sides: 7x > 77
-
Divide both sides by 7: x > 11
This means that any number greater than 11 satisfies the inequality.
Conclusion: A Foundation for Further Mathematical Exploration
The seemingly simple expression "seven times the difference of a number and 7" provides a rich foundation for exploring fundamental algebraic concepts. By understanding its components, translating it into mathematical notation, solving related equations and inequalities, and considering its variations and applications, we gain valuable insights into the power and versatility of mathematical expressions. This understanding forms a crucial stepping stone towards more advanced mathematical concepts and their real-world applications. The exploration of this single expression highlights the beauty and practical utility of mathematics, demonstrating how seemingly simple concepts can lead to a deeper appreciation of its broader significance. Furthermore, the ability to translate word problems into mathematical expressions is a crucial skill for success in various fields, underscoring the importance of mastering this fundamental concept.
Latest Posts
Latest Posts
-
Whats 4 To The Power Of 2
May 10, 2025
-
The Nonliving Parts Of An Ecosystem
May 10, 2025
-
What Is Another Name For A Regular Quadrilateral
May 10, 2025
-
Express The Fractions 1 2 3 16 And 7 8 With An Lcd
May 10, 2025
-
Find The Unit Vector In The Same Direction As V
May 10, 2025
Related Post
Thank you for visiting our website which covers about Seven Times The Difference Of A Number And 7. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.