Whats 4 To The Power Of 2
listenit
May 10, 2025 · 6 min read
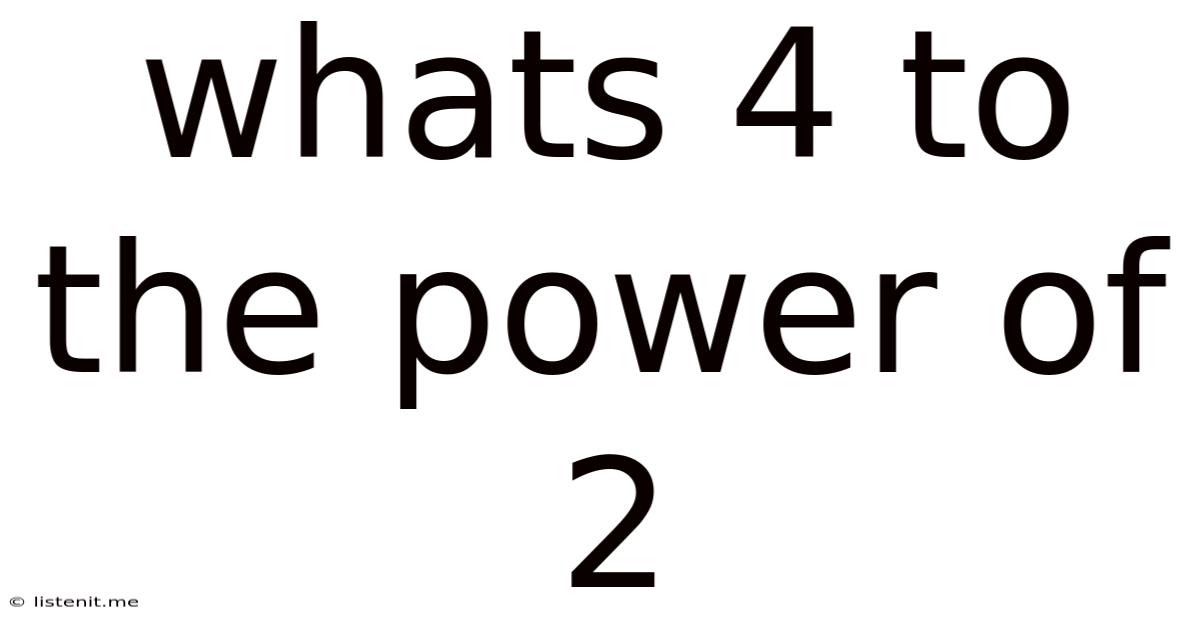
Table of Contents
What's 4 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What's 4 to the power of 2?" opens the door to a fascinating exploration of exponents, their properties, and their wide-ranging applications in mathematics, science, and everyday life. While the answer itself is straightforward – 16 – understanding the underlying concepts provides a solid foundation for more complex mathematical endeavors. This article will delve into the intricacies of exponents, exploring their definition, properties, and practical uses, all while keeping the fundamental question of 4² at the forefront.
Understanding Exponents: A Foundation for Calculation
In mathematics, an exponent (also called a power or index) is a number that indicates how many times a base number is multiplied by itself. It's written as a superscript to the right of the base number. For example, in the expression 4², the number 4 is the base, and the number 2 is the exponent. This expression is read as "4 raised to the power of 2" or "4 squared." It signifies that the base number (4) is multiplied by itself twice: 4 x 4 = 16.
Therefore, the answer to "What's 4 to the power of 2?" is 16. However, let's move beyond this simple calculation and explore the broader implications of exponents.
Beyond 4²: Exploring Different Exponents
The concept of exponents isn't limited to the power of 2. We can explore various exponents and their impact on the base number:
-
4¹ (4 to the power of 1): This simply means 4 multiplied by itself once, which equals 4. Any number raised to the power of 1 is the number itself.
-
4³ (4 to the power of 3): This is 4 multiplied by itself three times: 4 x 4 x 4 = 64. This is also known as "4 cubed."
-
4⁰ (4 to the power of 0): Any non-zero number raised to the power of 0 equals 1. Therefore, 4⁰ = 1. This might seem counterintuitive, but it's a fundamental rule in exponent mathematics.
-
4⁻¹ (4 to the power of -1): A negative exponent indicates the reciprocal of the base raised to the positive exponent. Therefore, 4⁻¹ = 1/4 = 0.25.
-
4⁻² (4 to the power of -2): This is the reciprocal of 4²: 1/4² = 1/16 = 0.0625.
Properties of Exponents: Rules for Simplification
Understanding the properties of exponents is crucial for simplifying complex expressions and solving equations. These properties allow us to manipulate exponential expressions efficiently. Let's explore some key properties:
-
Product of Powers: When multiplying two numbers with the same base, you can add their exponents. For example, 4² x 4³ = 4⁽²⁺³⁾ = 4⁵ = 1024.
-
Quotient of Powers: When dividing two numbers with the same base, you can subtract their exponents. For example, 4⁵ / 4² = 4⁽⁵⁻²⁾ = 4³ = 64.
-
Power of a Power: When raising a power to another power, you multiply the exponents. For example, (4²)³ = 4⁽²ˣ³⁾ = 4⁶ = 4096.
-
Power of a Product: When raising a product to a power, you raise each factor to that power. For example, (4 x 2)² = 4² x 2² = 16 x 4 = 64.
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power. For example, (4/2)² = 4²/2² = 16/4 = 4.
Real-World Applications of Exponents
The concept of exponents extends far beyond abstract mathematical exercises. They find practical applications in diverse fields:
1. Compound Interest: Growing Your Money
Exponents play a vital role in calculating compound interest, which is the interest earned on both the principal amount and accumulated interest. The formula for compound interest involves exponents, allowing you to determine the future value of an investment based on the principal, interest rate, and time period.
2. Population Growth: Modeling Biological Systems
Exponential growth models are often used to represent population growth in various biological systems. The population's size at a given time is expressed as a function of the initial population size, growth rate, and time, all using exponential relationships.
3. Radioactive Decay: Measuring Half-Life
In nuclear physics, radioactive decay is modeled using exponential functions. The half-life of a radioactive substance, the time it takes for half of the substance to decay, is directly related to exponential decay equations.
4. Computer Science: Understanding Data Structures and Algorithms
Exponents frequently appear in computer science when analyzing algorithm efficiency and data structure complexities. The time or space complexity of an algorithm is often expressed using Big O notation, which frequently involves exponential functions.
5. Physics: Describing Physical Phenomena
Exponents are fundamental to many physical laws and equations. For instance, the intensity of light decreases exponentially with distance, and gravitational force follows an inverse-square law (an exponential relationship).
6. Engineering: Designing Structures and Systems
Engineers utilize exponential functions in various contexts, including structural analysis, circuit design, and signal processing. Understanding exponential growth and decay is crucial for designing reliable and efficient systems.
Expanding on 4²: Exploring Higher Powers and Fractional Exponents
While 4² is relatively simple, exploring higher powers and fractional exponents provides a deeper understanding of exponential relationships.
Higher Powers of 4
Let's consider higher powers of 4:
- 4⁴ = 4 x 4 x 4 x 4 = 256
- 4⁵ = 4 x 4 x 4 x 4 x 4 = 1024
- 4⁶ = 4 x 4 x 4 x 4 x 4 x 4 = 4096
- and so on...
Observe the rapid growth of the result as the exponent increases. This demonstrates the powerful nature of exponential functions.
Fractional Exponents and Roots
Fractional exponents represent roots. For example:
- 4^(1/2) is the square root of 4, which is 2.
- 4^(1/3) is the cube root of 4, approximately 1.587.
- 4^(2/3) is the cube root of 4 squared, or (4²)^(1/3) = 16^(1/3) ≈ 2.52.
Fractional exponents significantly expand the range of values that can be expressed using exponential notation.
Conclusion: The Enduring Importance of Exponents
The seemingly simple question, "What's 4 to the power of 2?" has led us on a journey into the world of exponents. We've uncovered their definition, properties, and their far-reaching applications across numerous disciplines. From calculating compound interest to modeling radioactive decay, exponents are essential mathematical tools with real-world consequences. Understanding exponents provides a strong foundation for advanced mathematical studies and practical problem-solving in various fields. While the answer to our initial question is simply 16, the journey to understanding its significance has been far more profound. The power of 2, and indeed, all exponents, lies in their ability to describe and predict change and growth in a multitude of contexts.
Latest Posts
Latest Posts
-
How Many Protons Neutrons And Electrons In Neon
May 10, 2025
-
1 8 Hours In Hours And Minutes
May 10, 2025
-
What Is The Fraction Of 0 95
May 10, 2025
-
What Do Subscripts Represent In A Chemical Equation
May 10, 2025
-
What Is The Greatest Common Factor Of 27 And 81
May 10, 2025
Related Post
Thank you for visiting our website which covers about Whats 4 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.