Least Common Multiple Of 4 6 And 9
listenit
Mar 30, 2025 · 5 min read
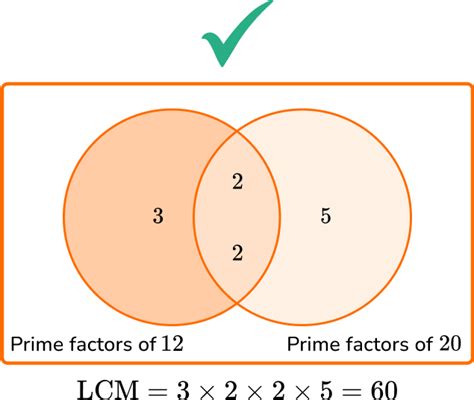
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with wide-ranging applications in various fields. This comprehensive guide will delve into the process of determining the LCM of 4, 6, and 9, exploring different methods and providing a thorough understanding of the underlying principles. We'll also touch upon the significance of LCMs and their practical use cases.
Understanding Least Common Multiples (LCMs)
Before diving into the calculation, let's establish a clear understanding of what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors. This concept is crucial in various mathematical operations and real-world problems.
Methods for Finding the LCM of 4, 6, and 9
There are several effective methods to calculate the LCM of 4, 6, and 9. We'll explore the most common and straightforward approaches:
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. While straightforward for smaller numbers, it becomes less efficient with larger numbers.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42...
- Multiples of 9: 9, 18, 27, 36, 45...
By inspecting the lists, we can see that the smallest common multiple is 36. Therefore, the LCM(4, 6, 9) = 36.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 4: 2²
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3²
To find the LCM, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
Multiplying these highest powers together gives us the LCM: 4 x 9 = 36. Thus, LCM(4, 6, 9) = 36. This method is generally more efficient and reliable, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of a set of numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. While less intuitive for multiple numbers, we can adapt this method. Let's first find the GCD of 4, 6, and 9 using the Euclidean algorithm or prime factorization:
- Prime factorization of 4: 2²
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3²
The only common factor is 1. Therefore, GCD(4, 6, 9) = 1. However, directly applying the LCM * GCD relationship is not as straightforward with three or more numbers. The prime factorization method remains more efficient in this case.
Applications of LCMs in Real-World Scenarios
The concept of LCM finds practical applications in diverse fields:
1. Scheduling and Time Management
Imagine you have three different cycles: one event repeats every 4 days, another every 6 days, and a third every 9 days. To determine when all three events will coincide, you need to find the LCM(4, 6, 9) = 36. All three events will coincide every 36 days. This principle is widely used in scheduling tasks, appointments, and coordinating events.
2. Measurement and Conversions
LCM is crucial in scenarios involving measurement conversions where you need to find a common denominator for different units. For example, if you're working with fractions involving 4, 6, and 9, finding the LCM helps simplify the calculations.
3. Fraction Operations
When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps to find the least common denominator (LCD), simplifying the process significantly. This makes calculations much easier and more efficient.
4. Gear Ratios and Mechanical Systems
In mechanical engineering, LCM is essential for calculating gear ratios and understanding the synchronization of rotating components within machines and systems. Understanding the cyclical nature of events using LCM is crucial for designing efficient and synchronized systems.
5. Music Theory and Rhythm
In music, LCM is applied in determining the least common denominator of various rhythmic patterns and note values. This ensures that different musical phrases synchronize correctly.
Expanding the Concept: LCMs of Larger Sets of Numbers
The methods described above can be extended to find the LCM of larger sets of numbers. The prime factorization method remains the most efficient approach for calculating the LCM of multiple numbers, regardless of their size. Simply find the prime factorization of each number, identify the highest power of each prime factor, and multiply those highest powers together to obtain the LCM.
Addressing Potential Challenges and Misconceptions
A common misconception is that the LCM is simply the largest number in the set. This is incorrect, as demonstrated by our example, where the LCM (36) is greater than the largest number (9). Always remember to utilize the appropriate method to correctly determine the LCM.
Another potential challenge is working with very large numbers. In such cases, utilizing a prime factorization calculator or mathematical software can streamline the process.
Conclusion: The Importance of Mastering LCM Calculations
Understanding and effectively calculating least common multiples is a fundamental skill with significant practical implications. Mastering different methods, like the prime factorization approach, empowers you to solve a wide range of problems across diverse fields, from scheduling to engineering and music. The ability to efficiently determine the LCM will significantly enhance your mathematical proficiency and problem-solving capabilities. This guide has provided a comprehensive understanding of the LCM of 4, 6, and 9, along with various methods and real-world applications. Remember, choosing the right method based on the numbers involved will optimize efficiency and accuracy in your calculations.
Latest Posts
Latest Posts
-
What Is 1 6 As A Percent
Apr 01, 2025
-
11 Is What Percent Of 97
Apr 01, 2025
-
What Are The Factors For 23
Apr 01, 2025
-
How Many Membranes Surround A Chloroplast
Apr 01, 2025
-
Find Unit Vector Orthogonal To Two Vectors
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 6 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
