Least Common Factor Of 12 And 36
listenit
Apr 04, 2025 · 5 min read
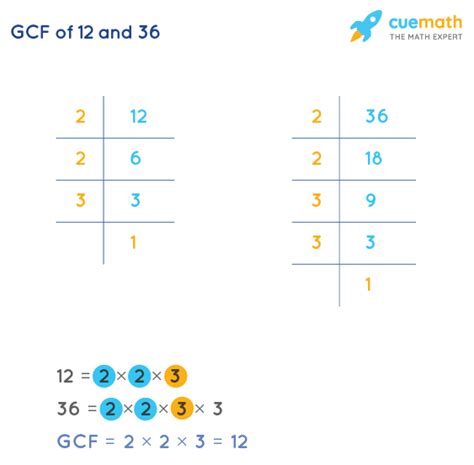
Table of Contents
Unveiling the Least Common Multiple (LCM) of 12 and 36: A Deep Dive into Number Theory
Finding the least common multiple (LCM) is a fundamental concept in number theory with wide-ranging applications in various fields, from scheduling problems to music theory. This comprehensive guide will explore the LCM of 12 and 36, delving into multiple methods for its calculation and highlighting the significance of this concept within the broader landscape of mathematics. We'll move beyond a simple answer and unpack the underlying principles, providing a thorough understanding you can apply to other LCM problems.
Understanding Least Common Multiples (LCM)
Before we dive into the specifics of 12 and 36, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. This contrasts with the greatest common divisor (GCD), which is the largest number that divides both integers without leaving a remainder.
Key Properties of LCM:
- Uniqueness: For any set of integers, there's only one LCM.
- Commutativity: The LCM of a and b is the same as the LCM of b and a. The order doesn't matter.
- Associativity: The LCM of (a, (b, c)) is the same as the LCM of ((a, b), c). This allows you to calculate the LCM of multiple numbers sequentially.
- Relationship with GCD: The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship is a powerful tool for calculating LCMs, as we'll see later.
Methods for Calculating the LCM of 12 and 36
Several methods exist for calculating the LCM of 12 and 36. Let's explore the most common approaches:
1. Listing Multiples Method
This is the most straightforward method, particularly for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both:
Multiples of 12: 12, 24, 36, 48, 60, 72... Multiples of 36: 36, 72, 108...
The smallest multiple appearing in both lists is 36. Therefore, the LCM(12, 36) = 36.
This method is simple for smaller numbers but becomes impractical for larger numbers or when dealing with more than two numbers.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 12: 2² x 3
- Prime factorization of 36: 2² x 3²
To find the LCM, we take the highest power of each prime factor present in either factorization:
LCM(12, 36) = 2² x 3² = 4 x 9 = 36
This method is generally preferred for its efficiency and applicability to larger numbers.
3. Using the GCD (Greatest Common Divisor)
As mentioned earlier, there's a direct relationship between the LCM and GCD of two numbers:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 12 and 36. We can use the Euclidean algorithm for this:
36 = 12 x 3 + 0
The remainder is 0, so the GCD(12, 36) = 12.
Now, we can use the formula:
LCM(12, 36) = (12 x 36) / GCD(12, 36) = (12 x 36) / 12 = 36
This method efficiently utilizes the relationship between LCM and GCD, making it a powerful tool for calculating LCMs.
Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. Its applications are diverse and impactful across several fields:
1. Scheduling Problems
Imagine you have two events that occur at regular intervals. One event happens every 12 days, and another every 36 days. When will both events occur on the same day again? The answer is the LCM(12, 36) = 36 days.
2. Music Theory
LCMs are used in music theory to determine the least common denominator of different note durations. This helps in harmonizing and composing musical pieces.
3. Gear Ratios
In mechanical engineering, LCM is used in calculating gear ratios and determining when gears will be perfectly synchronized.
4. Cyclic Processes
LCM is crucial in understanding and predicting the repetition of cyclic processes in various systems, from natural phenomena to industrial machinery.
5. Modular Arithmetic
LCM plays a significant role in modular arithmetic, a branch of number theory that is fundamental in cryptography and computer science.
Advanced Concepts and Extensions
While we've focused on the LCM of two integers, the concept extends to more than two numbers. To find the LCM of multiple numbers, you can apply the prime factorization method or repeatedly apply the two-number LCM method. For example, to find the LCM of 12, 36, and 60:
- Find the LCM of 12 and 36 (which is 36).
- Find the LCM of 36 and 60. The prime factorization method is efficient here.
- Prime factorization of 36: 2² x 3²
- Prime factorization of 60: 2² x 3 x 5
LCM(36, 60) = 2² x 3² x 5 = 180
Therefore, LCM(12, 36, 60) = 180
Conclusion: Mastering the LCM
Understanding the least common multiple is a fundamental building block in mathematics with surprisingly broad applications. This comprehensive guide has provided multiple methods for calculating the LCM, specifically for 12 and 36, and highlighted its significance in various fields. By mastering these techniques and understanding the underlying principles, you'll be well-equipped to tackle more complex problems and appreciate the elegance and power of number theory. Remember, the key is to choose the most efficient method based on the numbers involved, and always appreciate the interconnectedness of mathematical concepts – in this case, the relationship between LCM and GCD. The seemingly simple calculation of the LCM of 12 and 36 opens doors to a rich world of mathematical exploration and practical applications.
Latest Posts
Latest Posts
-
5 Over 9 As A Decimal
Apr 05, 2025
-
What Is 7 9 As A Percent
Apr 05, 2025
-
How Does Carbon Dioxide Enter A Leaf
Apr 05, 2025
-
How Many Moles Are 1 20 X 1025 Atoms Of Phosphorus
Apr 05, 2025
-
How Many Chromosomes In Each Daughter Cell
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Least Common Factor Of 12 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
