Is The Sine Function Even Or Odd
listenit
Mar 29, 2025 · 5 min read
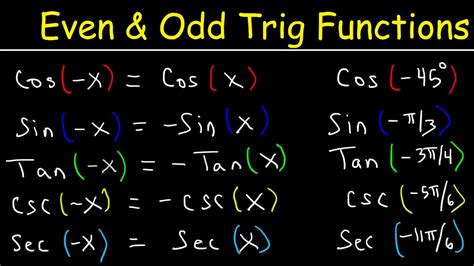
Table of Contents
Is the Sine Function Even or Odd? A Deep Dive into Trigonometric Identities
Determining whether the sine function is even or odd is a fundamental concept in trigonometry with far-reaching implications in various fields, from physics and engineering to computer graphics and signal processing. This comprehensive guide will not only answer the question definitively but also explore the underlying mathematical principles, provide practical examples, and delve into the broader significance of even and odd functions.
Understanding Even and Odd Functions
Before diving into the specifics of the sine function, let's establish a clear understanding of even and odd functions. A function is considered even if it satisfies the following condition:
f(-x) = f(x) for all x in the domain.
Graphically, an even function exhibits symmetry about the y-axis. This means that if you reflect the graph across the y-axis, it remains unchanged. Examples of even functions include f(x) = x², f(x) = cos(x), and f(x) = |x|.
Conversely, a function is considered odd if it satisfies this condition:
f(-x) = -f(x) for all x in the domain.
Odd functions exhibit symmetry about the origin. If you rotate the graph 180 degrees about the origin, it remains unchanged. Examples of odd functions include f(x) = x³, f(x) = sin(x), and f(x) = tan(x).
Proving the Sine Function is Odd
Now, let's rigorously prove that the sine function, sin(x), is indeed an odd function. We will utilize the unit circle definition of sine and the properties of trigonometric functions.
Recall that the sine of an angle x (in radians) is defined as the y-coordinate of the point on the unit circle corresponding to that angle. Let's consider an angle x and its negative counterpart, -x.
On the unit circle:
- sin(x): Represents the y-coordinate of a point on the unit circle.
- sin(-x): Represents the y-coordinate of the point obtained by rotating x radians in the clockwise direction.
Geometrically, these two points are reflections of each other across the x-axis. Since the y-coordinates of these points are opposites, we can conclude:
sin(-x) = -sin(x)
This equation perfectly aligns with the definition of an odd function. Therefore, we have definitively proven that the sine function is odd.
Graphical Representation
Visualizing the graph of y = sin(x) further solidifies this understanding. The graph is symmetric about the origin. If you were to rotate the graph 180 degrees about the origin, it would perfectly overlap itself. This visual symmetry is a hallmark of an odd function.
Implications of the Sine Function Being Odd
The odd nature of the sine function has significant repercussions in various mathematical and applied contexts:
-
Fourier Series: In signal processing and analysis, Fourier series decompose periodic functions into a sum of sine and cosine functions. The oddness of the sine function plays a crucial role in determining the coefficients of these series for odd functions.
-
Integration: When integrating sine functions over symmetric intervals, the odd symmetry simplifies the calculations. The integral of an odd function over a symmetric interval (e.g., from -a to a) is always zero.
-
Differential Equations: Many differential equations involving sine functions are greatly simplified by leveraging the odd nature of the function. This property often leads to elegant solutions and helps in understanding the behavior of systems modeled by these equations.
-
Physics and Engineering: The sine function is fundamental in describing oscillatory phenomena, such as simple harmonic motion (e.g., a pendulum's swing). Understanding its odd symmetry is vital in modeling these systems and predicting their behavior.
Comparing Sine and Cosine
It's helpful to compare the sine function with the cosine function, which is an even function. This contrast emphasizes the distinct properties of even and odd functions.
- Cosine (Even): cos(-x) = cos(x) – Symmetric about the y-axis.
- Sine (Odd): sin(-x) = -sin(x) – Symmetric about the origin.
This difference is reflected in their respective graphs and how they behave in various mathematical operations.
Practical Examples
Let's consider a few practical examples to illustrate the implications of the sine function being odd:
Example 1: Evaluating sin(-π/4)
Since sin(x) is odd, we can use the property sin(-x) = -sin(x):
sin(-π/4) = -sin(π/4) = -√2/2
Example 2: Integration
Let's consider the definite integral of sin(x) from -π to π:
∫<sub>-π</sub><sup>π</sup> sin(x) dx = 0
This result is a direct consequence of the sine function's odd symmetry. The positive and negative areas cancel each other out.
Example 3: Solving a Differential Equation
Consider a simple harmonic oscillator equation:
d²y/dt² + ω²y = 0
A solution to this equation is of the form y(t) = A sin(ωt), where A is the amplitude and ω is the angular frequency. The oddness of the sine function plays a role in understanding the oscillation's characteristics.
Beyond the Basics: Further Exploration
The oddness of the sine function forms a cornerstone for understanding more complex trigonometric identities and their applications. Exploring these identities deepens our understanding of the function's behavior and its significance in various fields.
Here are some avenues for further exploration:
-
Trigonometric Identities: Investigate identities involving sine functions, such as the sum-to-product formulas and the power-reduction formulas.
-
Complex Numbers: Explore the relationship between the sine function and complex exponentials using Euler's formula (e<sup>ix</sup> = cos(x) + i sin(x)).
-
Calculus: Study the derivatives and integrals of sine functions and how these operations interact with the function's odd symmetry.
-
Advanced Applications: Delve into the use of sine functions in fields like quantum mechanics, electromagnetism, and acoustics.
Conclusion
The question of whether the sine function is even or odd is not merely a theoretical exercise. It is a fundamental concept with profound implications across various branches of mathematics and its applications. By understanding the odd nature of the sine function, its symmetry, and its consequent properties, we gain a deeper appreciation of its role in describing oscillations, waves, and other crucial phenomena in the natural world and technology. This thorough investigation should leave you not only with a clear understanding of the sine function's oddity but also with a greater appreciation of its widespread importance.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 5 And 10
Apr 01, 2025
-
What Is 1 3 As A Percent
Apr 01, 2025
-
Why Does Transcription Occur In The Nucleus
Apr 01, 2025
-
What Is The Gcf Of 27 And 45
Apr 01, 2025
-
Compounds Containing Only Carbon And Hydrogen Are Called
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is The Sine Function Even Or Odd . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
