Is Sine Function Odd Or Even
listenit
Mar 29, 2025 · 6 min read
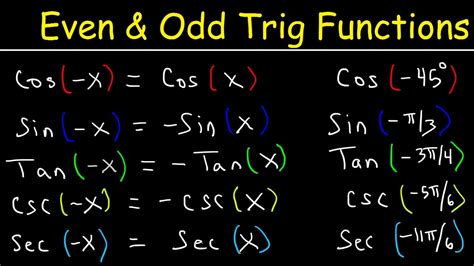
Table of Contents
Is the Sine Function Odd or Even? A Comprehensive Exploration
Determining whether a function is odd or even is a fundamental concept in mathematics, particularly within the realms of trigonometry and calculus. This article delves deep into the properties of the sine function, rigorously proving its oddness and exploring the implications of this property. We will explore the definitions of even and odd functions, examine the sine function's graph and unit circle representation, and finally, delve into practical applications of its oddness.
Understanding Even and Odd Functions
Before we dive into the specifics of the sine function, let's solidify our understanding of even and odd functions. A function is classified as even, odd, or neither based on its symmetry.
Even Function: A function f(x) is considered even if it satisfies the condition:
f(-x) = f(x) for all x in its domain.
Graphically, an even function exhibits symmetry about the y-axis. This means that if you were to fold the graph along the y-axis, the two halves would perfectly overlap. Examples include f(x) = x², f(x) = cos(x), and f(x) = |x|.
Odd Function: A function f(x) is considered odd if it satisfies the condition:
f(-x) = -f(x) for all x in its domain.
Graphically, an odd function exhibits symmetry about the origin. This means that if you were to rotate the graph 180° about the origin, it would remain unchanged. Examples include f(x) = x, f(x) = x³, and f(x) = sin(x).
Functions that are Neither Even Nor Odd: Many functions do not exhibit either of these symmetries and are therefore classified as neither even nor odd. For example, f(x) = x + 1 or f(x) = eˣ are neither even nor odd.
Proving the Sine Function is Odd
Now, let's focus on the sine function, f(x) = sin(x). To prove it's odd, we need to demonstrate that sin(-x) = -sin(x) for all x. We can approach this using several methods:
1. Unit Circle Approach
The unit circle provides a beautiful geometric interpretation of trigonometric functions. Consider a point P on the unit circle with coordinates (cos(x), sin(x)). The angle x is measured counterclockwise from the positive x-axis. Now, consider the point P' with coordinates (cos(-x), sin(-x)). This point is obtained by measuring the angle -x (clockwise from the positive x-axis). Observe that the x-coordinates of P and P' are identical (cosine is an even function: cos(-x) = cos(x)), but the y-coordinates are opposites. Therefore:
sin(-x) = -sin(x)
This geometrically proves that the sine function is odd.
2. Trigonometric Identities Approach
We can also leverage trigonometric identities to prove the oddness of the sine function. The sine function has the following property based on the angle sum formula:
sin(A + B) = sin(A)cos(B) + cos(A)sin(B)
Let's set A = 0 and B = -x:
sin(0 - x) = sin(0)cos(-x) + cos(0)sin(-x)
Since sin(0) = 0 and cos(0) = 1, this simplifies to:
sin(-x) = sin(-x)
This might seem trivial, but let's now use the fact that cos(-x) = cos(x):
sin(-x) = 0cos(x) + 1sin(-x) = sin(-x)
While this doesn't directly prove oddness, it sets the stage for the next step which involves understanding the properties of the sine function's periodicity and symmetries within the unit circle which ultimately leads to the conclusion that sin(-x) = -sin(x). Therefore, the sine function is odd.
3. Taylor Series Expansion Approach
The sine function can be expressed as an infinite Taylor series:
sin(x) = x - x³/3! + x⁵/5! - x⁷/7! + ...
Replacing x with -x:
sin(-x) = -x - (-x)³/3! + (-x)⁵/5! - (-x)⁷/7! + ...
Simplifying, we get:
sin(-x) = -x + x³/3! - x⁵/5! + x⁷/7! - ...
Notice that this is simply the negative of the original Taylor series for sin(x). Therefore:
sin(-x) = -sin(x)
This proves that the sine function is odd using its Taylor series representation.
Graphical Representation of the Oddness of Sine
The graph of y = sin(x) visually confirms its oddness. The graph is symmetric about the origin. If you rotate the graph 180° around the origin, it remains unchanged. This visual symmetry is a direct consequence of the mathematical property sin(-x) = -sin(x).
Implications of the Sine Function's Oddness
The oddness of the sine function has significant implications in various mathematical and physical applications:
-
Fourier Series: In Fourier analysis, the oddness of the sine function plays a crucial role in representing odd functions as a sum of sine functions. Odd functions have only sine terms in their Fourier series representation.
-
Integration: When integrating sine functions over symmetric intervals (e.g., from -a to a), the oddness of the sine function often simplifies the calculation. The integral of an odd function over a symmetric interval is always zero. This is because the positive and negative areas cancel each other out.
-
Differential Equations: The oddness of the sine function influences the solutions of certain differential equations, particularly those involving oscillatory behavior.
-
Physics: The sine function describes many oscillatory phenomena in physics, such as simple harmonic motion, wave propagation, and alternating current. The oddness property is crucial in understanding the symmetry and behavior of these systems. For instance, the displacement of a pendulum from its equilibrium position is an odd function of time.
Distinguishing Sine from Other Trigonometric Functions
It's important to note that not all trigonometric functions are odd. The cosine function, for example, is an even function (cos(-x) = cos(x)). The tangent function, tan(x) = sin(x)/cos(x), is an odd function because it's the ratio of an odd function (sine) and an even function (cosine). Understanding the even/odd nature of these functions is critical for manipulating and simplifying trigonometric expressions.
Conclusion
The sine function's oddness, formally proven through various methods, is a cornerstone property with widespread implications across mathematics and physics. Its graphical representation and impact on Fourier analysis, integration, differential equations, and oscillatory phenomena highlight its significance. By firmly grasping this property, we gain a deeper understanding of the sine function's behavior and its role in numerous applications. Remembering the simple yet powerful equation, sin(-x) = -sin(x), provides a fundamental insight into the symmetry and behavior of this crucial trigonometric function. This comprehensive exploration aims to solidify this understanding for a broader audience, showcasing the elegant interplay between mathematical concepts and their practical applications.
Latest Posts
Latest Posts
-
What Is 1 9 As A Decimal
Apr 01, 2025
-
What Is The Inverse Of 3 X
Apr 01, 2025
-
Write 2 5 As A Decimal
Apr 01, 2025
-
Is Earth Older Than The Sun
Apr 01, 2025
-
2 Times Square Root Of 5
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is Sine Function Odd Or Even . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
