Is Sin An Even Or Odd Function
listenit
Mar 27, 2025 · 5 min read
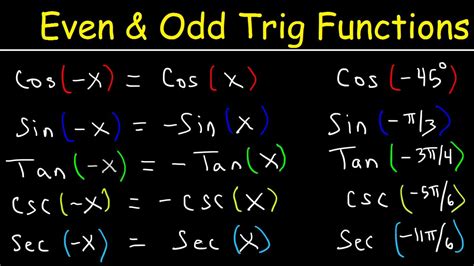
Table of Contents
Is Sin an Even or Odd Function? A Deep Dive into Trigonometric Identities
The question of whether the sine function is even or odd is a fundamental concept in trigonometry and calculus. Understanding this property is crucial for simplifying expressions, solving equations, and grasping more advanced mathematical concepts. This comprehensive guide will delve into the definition of even and odd functions, explore the properties of the sine function, and definitively answer the question, providing you with a robust understanding of this important topic. We'll also touch upon the practical applications of this knowledge.
Understanding Even and Odd Functions
Before we delve into the specifics of the sine function, let's clarify the definitions of even and odd functions. These classifications are based on the function's behavior when the input (the x-value) is replaced with its negative.
-
Even Function: A function f(x) is considered even if f(-x) = f(x) for all x in its domain. Graphically, an even function is symmetric about the y-axis. Classic examples include f(x) = x² and f(x) = cos(x).
-
Odd Function: A function f(x) is considered odd if f(-x) = -f(x) for all x in its domain. Graphically, an odd function exhibits rotational symmetry of 180 degrees about the origin. The function f(x) = x³ and f(x) = sin(x) are prime examples.
It's crucial to note that not all functions are either even or odd. Many functions possess neither of these symmetries.
Investigating the Sine Function: sin(x)
The sine function, denoted as sin(x), is a fundamental trigonometric function defined as the ratio of the opposite side to the hypotenuse in a right-angled triangle. However, its definition extends beyond right-angled triangles to encompass all real numbers, creating a periodic wave-like pattern. To determine whether sin(x) is even or odd, we need to examine its behavior when the input is negated.
Let's consider the unit circle, a circle with radius 1 centered at the origin. The sine of an angle x is represented by the y-coordinate of the point where the terminal side of the angle intersects the unit circle. Now, let's consider the angle -x. This angle is formed by rotating clockwise from the positive x-axis by an amount x. The y-coordinate of the point where the terminal side of -x intersects the unit circle is the negative of the y-coordinate for angle x.
Therefore, we can definitively state:
sin(-x) = -sin(x)
This identity holds true for all real values of x. Since sin(-x) = -sin(x) satisfies the definition of an odd function, we conclude that:
The sine function, sin(x), is an odd function.
Graphical Representation and Symmetry
Visualizing the graph of y = sin(x) reinforces this conclusion. The graph exhibits rotational symmetry about the origin. If you rotate the graph 180 degrees about the origin, it perfectly overlaps with itself. This visual symmetry directly corresponds to the mathematical property sin(-x) = -sin(x). This graphical representation provides an intuitive understanding of the odd nature of the sine function.
Proof Using the Unit Circle and Trigonometric Identities
We can also rigorously prove that sin(x) is an odd function using the unit circle definition and trigonometric identities. Recall that the sine function is defined as the y-coordinate of a point on the unit circle. When we consider the angle -x, we are reflecting the angle x across the x-axis. This reflection changes the sign of the y-coordinate but leaves the x-coordinate unchanged. Thus, sin(-x) = -sin(x). This provides a formal mathematical justification for the odd nature of the sine function.
Exploring the Sine Function's Oddness: Practical Implications
Understanding that the sine function is odd has significant implications in various areas of mathematics and its applications:
-
Simplification of Trigonometric Expressions: Knowing that sin(-x) = -sin(x) allows for the simplification of complex trigonometric expressions. This is particularly useful when solving trigonometric equations or identities.
-
Calculus: The oddness of the sine function plays a crucial role in integral calculus. For instance, the integral of an odd function over a symmetric interval (e.g., from -a to a) is always zero. This property simplifies many integration problems considerably.
-
Fourier Analysis: Fourier analysis uses trigonometric functions to decompose complex periodic signals into simpler sinusoidal components. Understanding the even/odd properties of these functions is vital for efficient signal processing and analysis.
-
Physics and Engineering: The sine function models many oscillatory phenomena in physics and engineering, such as simple harmonic motion, alternating current, and wave propagation. The oddness of the sine function influences the symmetry and behavior of these systems.
Distinguishing Sine from Cosine: Even vs. Odd
It's essential to contrast the sine function with the cosine function. While the sine function is odd, the cosine function is even. This means:
- cos(-x) = cos(x)
This difference in parity (even or odd) leads to different symmetries in their graphs and different behaviors in mathematical operations.
Advanced Applications and Further Exploration
The property of the sine function being odd extends to more advanced mathematical concepts. For example, in complex analysis, the sine function is an entire function (analytic across the entire complex plane), and its oddness is preserved in the complex domain. Furthermore, the oddness of sine is fundamental to understanding its Taylor series expansion, which provides an infinite polynomial representation of the function. The Taylor series expansion explicitly shows the odd powers of x in the series, directly reflecting the function's odd nature.
Conclusion: The Significance of Sin(x)'s Oddness
The conclusion is clear and unambiguous: the sine function, sin(x), is an odd function. This seemingly simple property has profound implications across mathematics, physics, engineering, and computer science. Understanding and utilizing this property is essential for mastering trigonometry, calculus, and numerous other fields. Its graphical symmetry, its role in simplifying expressions, and its impact on advanced mathematical concepts all highlight the significance of recognizing and applying the odd nature of the sine function. By grasping this fundamental concept, you'll be equipped with a powerful tool for tackling a wide range of mathematical and scientific problems.
Latest Posts
Latest Posts
-
What Is 70 Degrees In Fahrenheit In Celsius
Mar 30, 2025
-
What Concentration Of So32 Is In Equilibrium With Ag2so3 And
Mar 30, 2025
-
Which Bond Is The Most Polar
Mar 30, 2025
-
How Many Strings Are On A Cello
Mar 30, 2025
-
Is Work Equal To Kinetic Energy
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Is Sin An Even Or Odd Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
