Is Work Equal To Kinetic Energy
listenit
Mar 30, 2025 · 7 min read
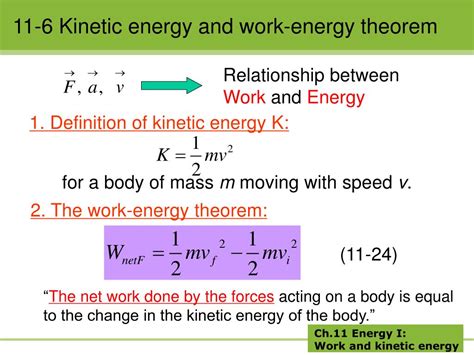
Table of Contents
Is Work Equal to Kinetic Energy? A Deep Dive into the Relationship Between Work and Energy
The relationship between work and kinetic energy is a cornerstone of classical mechanics. While the simple statement "work equals kinetic energy" is often used as a shorthand, it's a simplification that holds true only under specific conditions. This article will delve into the complexities of this relationship, exploring the nuances of work-energy theorems and clarifying the precise circumstances under which work directly translates into changes in kinetic energy.
Understanding Work and Kinetic Energy
Before exploring their relationship, let's define both terms precisely.
What is Work?
In physics, work is defined as the energy transferred to or from an object via the application of force along a displacement. It's a scalar quantity, meaning it has magnitude but no direction. The formula for work is:
W = Fd cosθ
Where:
- W represents work (measured in Joules)
- F represents the magnitude of the force applied (measured in Newtons)
- d represents the magnitude of the displacement (measured in meters)
- θ represents the angle between the force vector and the displacement vector
Crucially, work is only done if there's a component of force acting in the direction of the displacement. If the force is perpendicular to the displacement (θ = 90°), then cosθ = 0, and no work is done, regardless of the magnitude of the force. Think of carrying a heavy box horizontally – you're applying a force upward to counteract gravity, but you're not doing work on the box in the horizontal direction.
What is Kinetic Energy?
Kinetic energy is the energy an object possesses due to its motion. A stationary object has zero kinetic energy. The formula for kinetic energy is:
KE = 1/2mv²
Where:
- KE represents kinetic energy (measured in Joules)
- m represents the mass of the object (measured in kilograms)
- v represents the velocity of the object (measured in meters per second)
Kinetic energy is directly proportional to the mass and the square of the velocity. This means that doubling the velocity quadruples the kinetic energy.
The Work-Energy Theorem: The Bridge Between Work and Kinetic Energy
The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy. Mathematically:
W<sub>net</sub> = ΔKE = KE<sub>f</sub> - KE<sub>i</sub>
Where:
- W<sub>net</sub> represents the net work done (the sum of all work done by all forces acting on the object)
- ΔKE represents the change in kinetic energy
- KE<sub>f</sub> represents the final kinetic energy
- KE<sub>i</sub> represents the initial kinetic energy
This theorem is a fundamental principle in physics. It holds true regardless of the nature of the forces involved (conservative or non-conservative), as long as we consider the net work done.
Implications of the Work-Energy Theorem
The work-energy theorem clarifies the relationship between work and kinetic energy: work is not simply equal to kinetic energy, but rather to the change in kinetic energy. If an object starts at rest (KE<sub>i</sub> = 0) and a net work is done on it, then the work done is equal to its final kinetic energy. However, if the object already possesses kinetic energy, the work done will change its kinetic energy from its initial value to a final value.
Conservative vs. Non-Conservative Forces
The nature of the forces involved significantly impacts the application of the work-energy theorem.
-
Conservative forces: These forces, such as gravity and electrostatic forces, are path-independent. The work done by a conservative force depends only on the initial and final positions of the object, not the path taken. The work done by a conservative force can be stored as potential energy.
-
Non-conservative forces: These forces, such as friction and air resistance, are path-dependent. The work done by a non-conservative force depends on the path taken by the object. Energy is lost as heat or sound when non-conservative forces act.
In situations involving only conservative forces, the total mechanical energy (kinetic energy + potential energy) remains constant. However, when non-conservative forces are present, some mechanical energy is converted into other forms of energy (like heat), and the work-energy theorem accounts for this energy loss.
Examples Illustrating the Work-Energy Theorem
Let's consider some examples to illustrate the nuances of the work-energy relationship.
Example 1: A Block Sliding on a Frictionless Surface
Imagine a block sliding across a frictionless horizontal surface. A constant horizontal force is applied to the block, accelerating it. In this idealized scenario, the only force doing work is the applied force. The work done by this force is directly converted into an increase in the block's kinetic energy. The work-energy theorem directly applies: W = ΔKE.
Example 2: A Block Sliding on a Surface with Friction
Now, consider the same block sliding on a surface with friction. The applied force still does work, but now friction also does work, opposing the motion. The net work done is the difference between the work done by the applied force and the work done by friction. The net work is then equal to the change in kinetic energy. Because friction is a non-conservative force, some of the initial energy is lost as heat, resulting in a smaller change in kinetic energy than in the frictionless case.
Example 3: A Ball Thrown Vertically Upward
When a ball is thrown vertically upward, gravity does negative work on the ball as it rises, decreasing its kinetic energy and increasing its potential energy. At the highest point, the kinetic energy is zero, and the potential energy is maximum. As the ball falls, gravity does positive work, increasing the kinetic energy and decreasing the potential energy. Throughout the entire motion, the sum of kinetic and potential energy (mechanical energy) remains constant, ignoring air resistance.
Example 4: A Car Accelerating
Consider a car accelerating from rest. The engine provides a force that does positive work on the car, increasing its kinetic energy. However, other forces such as air resistance and friction in the car's components also do work, opposing the motion. The net work done on the car, taking into account all forces, equals the change in its kinetic energy.
When is Work NOT Equal to Kinetic Energy?
It's crucial to reiterate: the statement "work equals kinetic energy" is only true under very specific conditions. These conditions include:
- The object starts at rest: If the object initially has kinetic energy, the work done will change its kinetic energy from an initial non-zero value to a final value.
- Only one force is acting: If multiple forces act on the object, you must consider the net work done by all forces.
- No energy losses: The statement only holds true if there are no non-conservative forces (like friction) dissipating energy.
In most real-world scenarios, energy losses due to non-conservative forces are present. Therefore, the work-energy theorem, accounting for the change in kinetic energy and energy losses, provides a more accurate description of the system's energy transformations.
Conclusion: A Nuanced Understanding of the Work-Energy Relationship
The relationship between work and kinetic energy is fundamental to classical mechanics. While the simplified equation W = KE might be used informally, it's crucial to grasp the more comprehensive work-energy theorem: W<sub>net</sub> = ΔKE. This theorem accurately accounts for all forces acting on an object, including conservative and non-conservative forces, and reflects the change in kinetic energy, rather than just the final kinetic energy. A complete understanding of this relationship requires considering the initial and final kinetic energies, the nature of the forces involved, and the possibility of energy losses due to non-conservative forces. By acknowledging these nuances, we can accurately analyze and predict the motion of objects in various physical systems.
Latest Posts
Latest Posts
-
What Transition Metals Have A Fixed Charge
Apr 01, 2025
-
What Are Biotic Factors And Abiotic Factors
Apr 01, 2025
-
Common Multiples Of 4 And 9
Apr 01, 2025
-
How Many Quarts In 5 Gallon Bucket
Apr 01, 2025
-
What Is The Decimal For 11 20
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is Work Equal To Kinetic Energy . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
