Is An Equilateral Triangle An Isosceles Triangle
listenit
Apr 05, 2025 · 5 min read
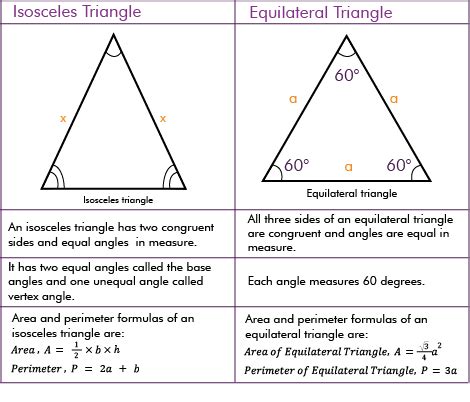
Table of Contents
Is an Equilateral Triangle an Isosceles Triangle? A Deep Dive into Triangle Classification
The question of whether an equilateral triangle is also an isosceles triangle often arises in geometry discussions. The answer, while seemingly simple, opens the door to a deeper understanding of triangle classification and the relationships between different triangle types. This article will explore this question thoroughly, examining the definitions of equilateral and isosceles triangles, exploring the logical implications, and providing visual representations to solidify the concept. We'll also delve into related concepts and explore why understanding this distinction is crucial for further geometrical studies.
Understanding Triangle Classification
Before diving into the specifics, let's establish a firm foundation in triangle classification. Triangles are classified based on their sides and angles. The primary classifications we'll focus on are:
-
Equilateral Triangles: These triangles have three sides of equal length and, consequently, three angles of equal measure (60° each). They are perfectly symmetrical.
-
Isosceles Triangles: These triangles have at least two sides of equal length, which are called legs. The angles opposite these equal sides are also equal. The third side is called the base.
-
Scalene Triangles: These triangles have no sides of equal length and therefore no angles of equal measure.
-
Right-Angled Triangles: These triangles have one angle that measures 90°. They can be isosceles, scalene, or even (though rarely discussed) right-angled equilateral. While not directly relevant to our primary question, understanding this classification adds context.
The Relationship: Equilateral and Isosceles
Now, let's address the core question: Is an equilateral triangle an isosceles triangle? The answer is a resounding yes.
Here's why:
The definition of an isosceles triangle states that it must have at least two sides of equal length. An equilateral triangle, by definition, has three sides of equal length. Since three is greater than two, an equilateral triangle perfectly satisfies the condition for being an isosceles triangle. It's a special case, a subset, of isosceles triangles.
Think of it like this: all squares are rectangles, but not all rectangles are squares. Similarly, all equilateral triangles are isosceles triangles, but not all isosceles triangles are equilateral triangles.
Visual Representation
Imagine you have a set of triangles. Within that set, you have a subset of isosceles triangles. Within the isosceles subset, you have an even smaller subset: the equilateral triangles. This visual representation illustrates the hierarchical relationship.
Triangles
├── Isosceles Triangles
│ └── Equilateral Triangles
└── Scalene Triangles
└── Right-Angled Triangles (can be isosceles, scalene, or right-angled equilateral)
This diagram clearly demonstrates that equilateral triangles are a specific type of isosceles triangle.
Logical Deduction and Set Theory
From a logical perspective, we can use set theory to represent the relationship:
Let:
- E represent the set of equilateral triangles.
- I represent the set of isosceles triangles.
Then, we can say that E ⊂ I, meaning that the set of equilateral triangles is a subset of the set of isosceles triangles. Every element (equilateral triangle) in set E is also an element in set I.
Why is this distinction important?
Understanding the relationship between equilateral and isosceles triangles is crucial for several reasons:
-
Formal Mathematical Reasoning: Recognizing this relationship strengthens your ability to apply logical deduction and set theory to geometrical problems.
-
Problem Solving: Knowing that an equilateral triangle possesses the properties of both equilateral and isosceles triangles allows you to apply a broader range of theorems and properties when solving problems.
-
Advanced Geometry: This foundational understanding is essential for tackling more complex geometrical concepts such as area calculations, trigonometric functions, and three-dimensional geometry. The properties of equilateral triangles form the basis for many advanced theorems and proofs.
-
Proof Writing: Being able to precisely define and differentiate between various triangle types is crucial when constructing formal geometric proofs.
Exploring Properties Shared by Equilateral and Isosceles Triangles
Both equilateral and isosceles triangles share some key properties:
-
At Least Two Equal Sides: As discussed, this is the defining characteristic of isosceles triangles, and equilateral triangles satisfy this condition.
-
At Least Two Equal Angles: The angles opposite the equal sides are equal in both types of triangles. In equilateral triangles, all three angles are equal (60°).
-
Symmetry: While equilateral triangles exhibit perfect three-fold rotational symmetry, isosceles triangles possess a line of symmetry through the base and the apex (the point opposite the base).
Distinguishing Features: What makes an Equilateral Triangle Unique?
Although an equilateral triangle is a type of isosceles triangle, it possesses unique characteristics that set it apart:
-
Three Equal Sides: This is the defining characteristic that distinguishes it from other isosceles triangles.
-
Three Equal Angles (60° each): This directly results from the equal side lengths.
-
Perfect Symmetry: It exhibits higher order symmetry compared to a general isosceles triangle.
Further Exploration: Related Concepts
Understanding the relationship between equilateral and isosceles triangles opens doors to exploring other related concepts, such as:
-
The Isosceles Triangle Theorem: This theorem states that the angles opposite the equal sides of an isosceles triangle are equal. This theorem applies to equilateral triangles as well.
-
Centroids, Incenters, and Circumcenters: The properties of these points within a triangle are influenced by the triangle's classification. Equilateral triangles exhibit unique properties related to these points.
-
Area Calculations: The formulas for calculating the area of triangles can be simplified when dealing with equilateral triangles due to their inherent symmetry.
Conclusion: A Crucial Understanding
The answer to the question, "Is an equilateral triangle an isosceles triangle?" is definitively yes. This seemingly straightforward answer unlocks a deeper understanding of triangle classification, logical deduction, and set theory within the context of geometry. Recognizing this relationship is fundamental for building a strong foundation in mathematics and tackling more advanced geometrical concepts. It's a cornerstone of understanding the intricate world of shapes and their properties. The ability to clearly define and differentiate between triangle types is not just a matter of rote memorization; it's a key skill for clear mathematical communication and successful problem-solving. This knowledge empowers you to navigate more complex geometrical challenges with confidence and precision.
Latest Posts
Latest Posts
-
X 1 X 1 X 1
Apr 06, 2025
-
What Is The Least Common Multiple Of 30 And 20
Apr 06, 2025
-
Chemical Reaction Between Hcl And Naoh
Apr 06, 2025
-
What Is 0 375 As A Percent
Apr 06, 2025
-
What Is The Final Product Of Dna Replication
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Is An Equilateral Triangle An Isosceles Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
