Is 6 7 A Rational Number
listenit
Apr 01, 2025 · 5 min read
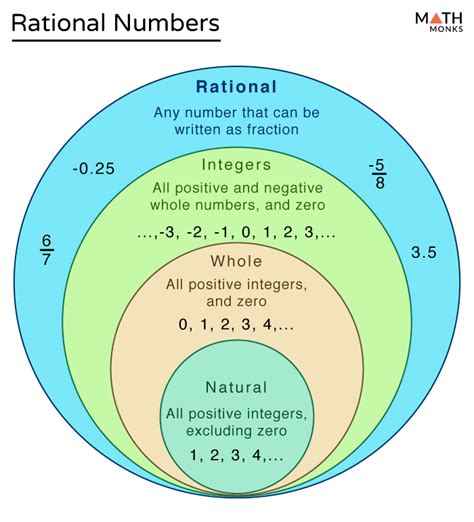
Table of Contents
Is 6/7 a Rational Number? A Deep Dive into Rational and Irrational Numbers
The question, "Is 6/7 a rational number?" seems simple at first glance. However, understanding the answer requires a solid grasp of the definitions of rational and irrational numbers. This article will not only answer this specific question but also provide a comprehensive exploration of rational and irrational numbers, their properties, and how to identify them. We'll delve into the historical context, provide practical examples, and explore the significance of these number classifications in mathematics.
Understanding Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. In simpler terms, it's any number that can be written as a fraction. The key characteristics are:
- Integers: The numerator (p) and the denominator (q) must be integers. Integers include whole numbers (0, 1, 2, 3...) and their negative counterparts (-1, -2, -3...).
- Non-zero denominator: The denominator (q) cannot be zero. Division by zero is undefined in mathematics.
Examples of Rational Numbers:
- 1/2: A classic example of a rational number.
- 3/4: Another simple fraction.
- -5/2: Negative fractions are also rational.
- 7: The whole number 7 can be expressed as 7/1, satisfying the definition.
- 0: Zero can be expressed as 0/1, making it a rational number.
- 0.75: This decimal can be expressed as the fraction 3/4.
- -2.5: This decimal can be expressed as the fraction -5/2.
Recurring Decimals as Rational Numbers:
A crucial point to understand is that recurring decimals (decimals with a repeating pattern) are always rational numbers. For instance, 0.333... (0.3 recurring) is equal to 1/3. Similarly, 0.142857142857... (0.142857 recurring) is equal to 1/7. These repeating patterns can always be converted into fractions, solidifying their status as rational numbers.
Understanding Irrational Numbers
Irrational numbers, in contrast to rational numbers, cannot be expressed as a fraction p/q where p and q are integers and q is not zero. Their decimal representations are non-terminating and non-repeating. This means the decimal goes on forever without any repeating pattern.
Examples of Irrational Numbers:
- π (Pi): The ratio of a circle's circumference to its diameter. Its decimal representation is approximately 3.14159..., but it continues infinitely without repetition.
- √2 (Square root of 2): This is the number that, when multiplied by itself, equals 2. It cannot be expressed as a simple fraction.
- e (Euler's number): The base of the natural logarithm. Approximately 2.71828..., it also continues infinitely without repetition.
- φ (Golden Ratio): Approximately 1.61803..., another irrational number with a significant presence in mathematics and art.
Back to the Main Question: Is 6/7 a Rational Number?
Given our definitions, the answer is a resounding yes. 6/7 perfectly fits the definition of a rational number. Both 6 and 7 are integers, and the denominator (7) is not zero. Therefore, 6/7 is unequivocally a rational number.
Further Exploration of Rational and Irrational Numbers
The distinction between rational and irrational numbers is fundamental to the structure of the real number system. Let's delve deeper into their properties and implications:
1. The Real Number System:
Rational and irrational numbers together form the set of real numbers. Real numbers encompass all numbers that can be plotted on a number line, including positive and negative numbers, zero, fractions, decimals, and irrational numbers.
2. Density of Rational and Irrational Numbers:
Both rational and irrational numbers are dense. This means that between any two distinct rational numbers, there exists another rational number, and similarly, between any two distinct irrational numbers, there exists another irrational number. This implies an infinite number of both rational and irrational numbers between any two given numbers.
3. Countability and Uncountability:
While both rational and irrational numbers are infinite, they differ significantly in their cardinality (size). The set of rational numbers is countable, meaning its elements can be put into a one-to-one correspondence with the natural numbers (1, 2, 3...). However, the set of irrational numbers is uncountable, meaning it's impossible to create such a correspondence. This difference highlights a profound distinction in the nature of these number sets.
4. Operations on Rational and Irrational Numbers:
-
Addition and Subtraction: The sum or difference of two rational numbers is always rational. However, the sum or difference of a rational and an irrational number is always irrational. The sum or difference of two irrational numbers can be either rational or irrational.
-
Multiplication and Division: The product or quotient of two rational numbers (excluding division by zero) is always rational. The product or quotient of a non-zero rational number and an irrational number is always irrational. The product or quotient of two irrational numbers can be either rational or irrational.
Practical Applications and Significance
Understanding the difference between rational and irrational numbers is not just an academic exercise; it has significant practical implications in various fields:
-
Engineering and Physics: Precise calculations in engineering and physics often require dealing with irrational numbers like π, especially in areas involving circles, spheres, and wave phenomena.
-
Computer Science: Representing irrational numbers in computers requires approximations, since computers can only store a finite number of digits. The choice of approximation method significantly influences the accuracy of calculations.
-
Finance and Economics: Irrational numbers can appear in financial models, particularly those involving continuous growth or decay.
-
Geometry and Trigonometry: Irrational numbers are fundamental to geometric calculations, particularly those involving angles and distances.
Conclusion
The simple question, "Is 6/7 a rational number?" serves as a springboard to explore the rich and nuanced world of rational and irrational numbers. By understanding their definitions, properties, and practical applications, we gain a deeper appreciation for the fundamental building blocks of the real number system and their crucial role in mathematics and various scientific disciplines. The answer, as we've established, is definitively yes, 6/7 is a rational number, and this understanding forms the bedrock of further mathematical explorations. The contrast between rational and irrational numbers underscores the complexity and elegance inherent in the mathematical universe.
Latest Posts
Latest Posts
-
What Is 2 5 8 In Decimal Form
Apr 03, 2025
-
How Many Atoms Are In O2
Apr 03, 2025
-
What Are The Subunits Of Nucleic Acids
Apr 03, 2025
-
Circumference Of A Circle With Diameter Of 8
Apr 03, 2025
-
What Is The Correct Formula For Aluminum Oxide
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Is 6 7 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
