Is 1 9 A Rational Number
listenit
Apr 05, 2025 · 4 min read
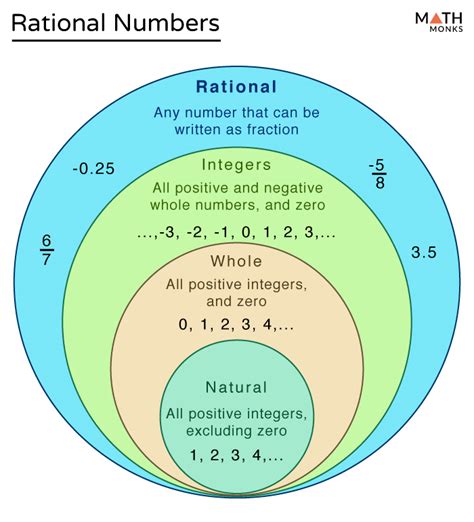
Table of Contents
Is 1/9 a Rational Number? A Deep Dive into Rational Numbers and Their Properties
The question, "Is 1/9 a rational number?" might seem simple at first glance. However, understanding the answer requires a deeper understanding of what constitutes a rational number and the properties that define them. This article will delve into the concept of rational numbers, exploring their characteristics, providing examples, and definitively answering whether 1/9 fits the criteria. We'll also explore related concepts and address common misconceptions.
Understanding Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the denominator, and q is not zero. This definition is crucial because it establishes the fundamental characteristic of rational numbers: their ability to be represented as a simple fraction.
Key Characteristics of Rational Numbers:
- Expressible as a fraction: This is the defining characteristic. If a number can be written as a fraction of two integers (with a non-zero denominator), it's rational.
- Terminating or repeating decimals: When expressed in decimal form, rational numbers either terminate (end) or have a repeating pattern of digits. For example, 1/4 = 0.25 (terminating), and 1/3 = 0.3333... (repeating).
- Inclusivity: Rational numbers include integers (which can be expressed as fractions with a denominator of 1), whole numbers, and fractions.
Examples of Rational Numbers:
- 1/2: This is a classic example. It's a simple fraction of two integers.
- -3/4: Negative fractions are also rational.
- 5: This integer can be written as 5/1.
- 0.75: This terminating decimal is rational because it can be expressed as 3/4.
- 0.666...: This repeating decimal is rational; it's equivalent to 2/3.
Irrational Numbers: The Counterpart
To fully grasp the concept of rational numbers, it's essential to understand their counterpart: irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating.
Examples of Irrational Numbers:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159..., continues infinitely without a repeating pattern.
- √2 (the square root of 2): This number cannot be expressed as a fraction of two integers.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828..., is another example.
Determining if 1/9 is Rational
Now, let's address the central question: Is 1/9 a rational number? The answer is a resounding yes. Here's why:
-
It's a fraction: 1/9 is already expressed as a fraction. The numerator (1) and the denominator (9) are both integers.
-
Decimal Representation: To further solidify this, let's convert 1/9 to a decimal:
1 ÷ 9 = 0.111111...
This is a repeating decimal (0.1 recurring), which is a characteristic of rational numbers.
Therefore, 1/9 satisfies the definition of a rational number. It can be expressed as a fraction of two integers, and its decimal representation is a repeating decimal.
Common Misconceptions about Rational Numbers
Several misconceptions can arise when dealing with rational numbers. Let's address some of them:
- All decimals are irrational: This is false. Terminating decimals and repeating decimals are rational. Only non-terminating and non-repeating decimals are irrational.
- Fractions must be proper: Improper fractions (where the numerator is larger than the denominator) are still rational. For example, 7/3 is a rational number.
- Only simple fractions are rational: Complex fractions (fractions within fractions) can also be simplified to rational numbers if their components are integers.
Further Exploration of Rational Numbers and Their Applications
Rational numbers form the basis of many mathematical concepts and have wide-ranging applications in various fields:
- Arithmetic: The fundamental operations of addition, subtraction, multiplication, and division are seamlessly performed with rational numbers.
- Algebra: Rational numbers are extensively used in solving algebraic equations and inequalities.
- Geometry: Rational numbers play a significant role in geometric calculations, such as finding the area and perimeter of shapes.
- Calculus: Rational functions (functions where both the numerator and denominator are polynomials) are a crucial part of calculus.
- Computer Science: Representing and manipulating rational numbers is essential in computer programming, especially in applications involving precise calculations.
- Real-World Applications: Rational numbers are ubiquitous in daily life, from measuring quantities (e.g., 1/2 cup of flour) to calculating financial transactions (e.g., expressing interest rates).
Conclusion
The question, "Is 1/9 a rational number?" serves as a springboard for exploring the broader concept of rational numbers. We've established that 1/9 unequivocally fits the definition, being expressible as a fraction of two integers and possessing a repeating decimal representation. Understanding rational numbers and their properties is crucial for a firm grasp of many mathematical concepts and their practical applications across various fields. By differentiating between rational and irrational numbers, we gain a more comprehensive understanding of the number system and its intricate workings. Remember the key characteristics—the ability to be expressed as a fraction of two integers, resulting in either a terminating or repeating decimal—and you'll be well-equipped to identify rational numbers confidently.
Latest Posts
Latest Posts
-
What Percent Of 50 Is 15
Apr 05, 2025
-
Write An Exponential Function Given Two Points Calculator
Apr 05, 2025
-
What Percent Of 752 Is 25
Apr 05, 2025
-
Difference Between Strong Base And Weak Base
Apr 05, 2025
-
What Does An Exclamation Mark Mean In Math
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Is 1 9 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
