Integral Of X 3 Sqrt X 2 1
listenit
Mar 24, 2025 · 5 min read
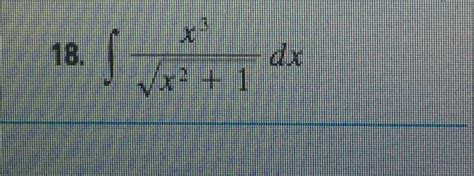
Table of Contents
Evaluating the Integral of x³√(x² + 1)
The integral ∫x³√(x² + 1) dx presents a fascinating challenge in calculus. It's not immediately obvious how to approach this, but with a strategic substitution, we can transform it into a much more manageable form. This article will guide you through the process of solving this integral, exploring various techniques and offering a comprehensive understanding of the solution.
Understanding the Problem
The integral ∫x³√(x² + 1) dx involves a combination of a polynomial term (x³) and a radical expression (√(x² + 1)). Direct integration isn't feasible. We need a substitution that simplifies the expression, allowing us to apply standard integration rules.
The Power of Substitution: Unveiling the Solution
The key to solving this integral lies in a clever substitution. Notice that the derivative of (x² + 1) is 2x. This suggests a substitution involving u = x² + 1. Let's explore this further:
Step 1: The Substitution
Let's substitute:
- u = x² + 1
This implies:
- du = 2x dx
Now, we need to express x³ in terms of u. From u = x² + 1, we can solve for x²:
- x² = u - 1
Therefore, we can rewrite x³ as:
- x³ = x²(x) = (u - 1)x
Step 2: Rewriting the Integral
Substituting these expressions into our original integral, we get:
∫x³√(x² + 1) dx = ∫(u - 1)x √u (du / 2x)
Notice that the 'x' term cancels out, significantly simplifying the expression:
∫(u - 1)√u (du / 2) = (1/2) ∫(u - 1)u<sup>1/2</sup> du
Step 3: Expanding and Integrating
Now we have a much simpler integral:
(1/2) ∫(u<sup>3/2</sup> - u<sup>1/2</sup>) du
Applying the power rule of integration (∫x<sup>n</sup> dx = (x<sup>n+1</sup>)/(n+1) + C), we get:
(1/2) [(u<sup>5/2</sup>) / (5/2) - (u<sup>3/2</sup>) / (3/2)] + C
Simplifying:
(1/2) [(2/5)u<sup>5/2</sup> - (2/3)u<sup>3/2</sup>] + C
(1/5)u<sup>5/2</sup> - (1/3)u<sup>3/2</sup> + C
Step 4: Back-Substitution
Finally, we substitute back u = x² + 1:
(1/5)(x² + 1)<sup>5/2</sup> - (1/3)(x² + 1)<sup>3/2</sup> + C
This is our final answer. It represents the indefinite integral of x³√(x² + 1) dx.
Understanding the Constant of Integration (C)
The constant of integration, 'C', is crucial. It represents the family of curves that share the same derivative. Since the derivative of a constant is zero, adding any constant to the antiderivative doesn't change its derivative.
Verification through Differentiation
To verify our solution, we can differentiate the result and see if we obtain the original integrand:
Let's differentiate (1/5)(x² + 1)<sup>5/2</sup> - (1/3)(x² + 1)<sup>3/2</sup> + C with respect to x:
d/dx [(1/5)(x² + 1)<sup>5/2</sup> - (1/3)(x² + 1)<sup>3/2</sup> + C]
Using the chain rule:
(1/5) * (5/2)(x² + 1)<sup>3/2</sup> * (2x) - (1/3) * (3/2)(x² + 1)<sup>1/2</sup> * (2x)
Simplifying:
x(x² + 1)<sup>3/2</sup> - x(x² + 1)<sup>1/2</sup>
Factoring out x(x² + 1)<sup>1/2</sup>:
x(x² + 1)<sup>1/2</sup> [ (x² + 1) - 1]
x(x² + 1)<sup>1/2</sup> (x²)
x³(x² + 1)<sup>1/2</sup>
This matches our original integrand, confirming the accuracy of our solution.
Alternative Approaches and Considerations
While the substitution method presented above is efficient, it's worth noting that other approaches might be considered, depending on the context and individual preferences. For instance, trigonometric substitution could also be employed, though it might lead to a more complex intermediate calculation. The choice of method often depends on familiarity and the specific characteristics of the integral.
Expanding the Knowledge: Definite Integrals
The solution we derived is an indefinite integral. To calculate a definite integral, we would evaluate the antiderivative at the upper and lower limits of integration and find the difference. For example, if we wanted to find the definite integral from 0 to 1, we would substitute these values into our solution and subtract the results. Remember that the constant of integration (C) cancels out when evaluating definite integrals.
Practical Applications and Further Exploration
Understanding techniques for solving integrals like this one is fundamental in various fields, including physics, engineering, and economics. Many real-world problems involve calculating areas, volumes, and other quantities that require integration. This specific integral, while seemingly abstract, might find applications in problems related to curves and volumes defined by specific functions.
Furthermore, exploring more complex integrals involving similar structures, perhaps with higher powers of x or different radical expressions, will deepen your understanding of integration techniques and broaden your problem-solving skills. Mastering integral calculus opens doors to a deeper understanding of the mathematical relationships that underpin many aspects of our world.
Conclusion
Solving the integral ∫x³√(x² + 1) dx requires strategic application of substitution. By carefully choosing a substitution and employing algebraic manipulation, we can transform a seemingly intractable integral into a simpler form that can be readily integrated using standard techniques. The step-by-step approach outlined in this article provides a clear and thorough method for solving this specific integral and demonstrates a broader approach that can be applied to other complex integration problems. Remember to always verify your solution through differentiation to ensure accuracy. Through practice and continued exploration, you'll strengthen your understanding of integral calculus and its powerful applications.
Latest Posts
Latest Posts
-
Is Electron Affinity The Same As Electronegativity
Mar 29, 2025
-
What Is The Expected Response To The Triceps Jerk Reflex
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Integral Of X 3 Sqrt X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
