Integral Of Sin 2x X 2
listenit
Mar 30, 2025 · 4 min read
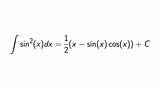
Table of Contents
Decoding the Integral of sin(2x) * x²: A Comprehensive Guide
The integral of sin(2x) * x², denoted as ∫x²sin(2x)dx, presents a fascinating challenge in calculus. It's not a straightforward integral that can be solved using simple substitution or basic integration formulas. Instead, it requires the application of a powerful technique known as integration by parts. This comprehensive guide will dissect this integral step-by-step, providing a clear understanding of the process and exploring related concepts.
Understanding Integration by Parts
Before diving into the integral itself, let's solidify our understanding of integration by parts. This technique is derived from the product rule of differentiation. Recall that the product rule states:
d(uv)/dx = u(dv/dx) + v(du/dx)
Integrating both sides with respect to x, we get:
∫d(uv)/dx dx = ∫u(dv/dx) dx + ∫v(du/dx) dx
This simplifies to:
uv = ∫u(dv/dx) dx + ∫v(du/dx) dx
Rearranging the equation, we obtain the integration by parts formula:
∫u(dv/dx) dx = uv - ∫v(du/dx) dx
The key to successfully applying integration by parts lies in strategically choosing the 'u' and 'dv/dx' terms. A common mnemonic device used is LIATE, which prioritizes the order of functions for 'u':
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions (polynomials like x², x³, etc.)
- Trigonometric functions (sin(x), cos(x), etc.)
- Exponential functions (eˣ, aˣ, etc.)
Applying Integration by Parts to ∫x²sin(2x)dx
Now, let's tackle the integral ∫x²sin(2x)dx using integration by parts. Following the LIATE rule, we choose:
- u = x² (Algebraic function)
- dv/dx = sin(2x) (Trigonometric function)
Now we need to find du/dx and v:
- du/dx = 2x
- v = -cos(2x)/2 (Remember to integrate dv/dx)
Substituting these values into the integration by parts formula, we get:
∫x²sin(2x)dx = x²(-cos(2x)/2) - ∫(-cos(2x)/2)(2x) dx
Simplifying, we have:
∫x²sin(2x)dx = -x²cos(2x)/2 + ∫xcos(2x) dx
Notice that we've reduced the power of 'x' from x² to x. However, we still have another integral to solve: ∫xcos(2x) dx. This requires another application of integration by parts.
Second Application of Integration by Parts
Let's apply integration by parts again to solve ∫xcos(2x) dx. We choose:
- u = x
- dv/dx = cos(2x)
Therefore:
- du/dx = 1
- v = sin(2x)/2
Substituting into the integration by parts formula:
∫xcos(2x) dx = x(sin(2x)/2) - ∫(sin(2x)/2)(1) dx
Simplifying:
∫xcos(2x) dx = xsin(2x)/2 - (1/2)∫sin(2x) dx
Now, we can easily integrate ∫sin(2x) dx:
∫sin(2x) dx = -cos(2x)/2
Combining the Results
Now let's substitute this result back into our original equation:
∫xcos(2x) dx = xsin(2x)/2 - (1/2)(-cos(2x)/2) ∫xcos(2x) dx = xsin(2x)/2 + cos(2x)/4
Substitute this back into the equation from our first integration by parts:
∫x²sin(2x)dx = -x²cos(2x)/2 + xsin(2x)/2 + cos(2x)/4 + C
Therefore, the final solution to the integral ∫x²sin(2x)dx is:
∫x²sin(2x)dx = (-x²cos(2x)/2) + (xsin(2x)/2) + (cos(2x)/4) + C
where 'C' is the constant of integration.
Verification through Differentiation
A crucial step in solving integrals is verification. We can check our answer by differentiating the result with respect to x. If we obtain the original integrand, x²sin(2x), then our solution is correct. This process involves applying the product rule and chain rule of differentiation, which is left as an exercise for the reader. The result should verify the accuracy of our integration.
Exploring Related Integrals and Techniques
This example highlights the power and versatility of integration by parts, particularly when dealing with integrals involving products of algebraic and trigonometric functions. Similar techniques can be applied to solve integrals like:
- ∫x³cos(3x)dx
- ∫x²eˣ dx
- ∫xln(x) dx
These integrals also require multiple applications of integration by parts, strategically choosing 'u' and 'dv/dx' in each step to simplify the integral progressively. The choice of 'u' and 'dv/dx' often significantly impacts the complexity of the solution.
Tabular Integration: A Streamlined Approach
For integrals involving products of a polynomial and a trigonometric or exponential function, a more efficient method called tabular integration can be utilized. This method systematically organizes the repeated applications of integration by parts in a tabular format, reducing the potential for errors in complex integrals.
The tabular method simplifies the process significantly, especially when dealing with higher-order polynomials. It's a recommended technique to explore for efficiency and accuracy in solving such integrals.
Conclusion: Mastering Integration Techniques
The integral of sin(2x) * x² serves as a valuable case study in mastering integration by parts. Through careful selection of 'u' and 'dv/dx', and systematic application of the formula, we successfully determined the integral. Remember to always verify your solution through differentiation to ensure accuracy. This exercise not only reinforces integration by parts but also introduces the concept of tabular integration, offering a streamlined approach for solving complex integrals. By mastering these techniques, you can effectively tackle a wider range of integration problems encountered in calculus and related fields. Remember that practice is key to solidifying these concepts.
Latest Posts
Latest Posts
-
What Is 1 6 As A Percent
Apr 01, 2025
-
11 Is What Percent Of 97
Apr 01, 2025
-
What Are The Factors For 23
Apr 01, 2025
-
How Many Membranes Surround A Chloroplast
Apr 01, 2025
-
Find Unit Vector Orthogonal To Two Vectors
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Integral Of Sin 2x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
