How To Get Rid Of Fractions
listenit
Apr 05, 2025 · 6 min read
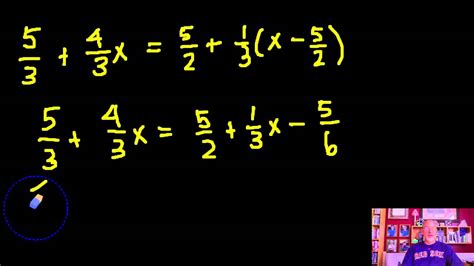
Table of Contents
How to Get Rid of Fractions: A Comprehensive Guide
Fractions. Those pesky little numbers that represent parts of a whole can be a source of frustration for many. Whether you're tackling a complex algebraic equation or simply trying to bake a cake, knowing how to effectively manipulate and eliminate fractions is crucial. This comprehensive guide will delve into various methods for getting rid of fractions, covering everything from basic arithmetic to advanced algebraic techniques. We’ll explore when eliminating fractions is beneficial, and when it might be better to leave them be. Let's dive in!
Understanding Fractions: A Quick Recap
Before we jump into eliminating fractions, let's refresh our understanding of what they represent. A fraction is simply a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the number of equal parts a whole is divided into, while the numerator indicates how many of those parts we're considering. For example, in the fraction 3/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (3) means we're taking three of those parts.
When Should You Eliminate Fractions?
The decision to eliminate fractions depends entirely on the context. In some cases, eliminating them simplifies calculations and makes problems easier to solve. In other instances, leaving fractions might be more efficient or even necessary. Here's a breakdown:
-
Simplification of Calculations: Eliminating fractions can drastically simplify arithmetic operations like addition, subtraction, multiplication, and division, especially when dealing with multiple fractions simultaneously. This leads to cleaner calculations and reduces the chance of errors.
-
Solving Equations: In algebra, eliminating fractions is often a critical first step in solving equations. It helps to clear the denominators, leaving a simpler equation that's easier to manipulate and solve.
-
Working with Real-World Problems: Many real-world applications involve fractions, like measuring ingredients in cooking or calculating areas and volumes. Eliminating fractions can provide clearer and more readily usable results in these situations.
-
When Fractions are Unnecessary: Sometimes, a fraction is simply not the most practical way to represent a quantity. For example, if you're dealing with money, it's often simpler to express amounts in decimal form rather than fractions of a dollar.
-
When Fractions are Useful: Conversely, leaving fractions might sometimes be preferable. Fractions can often provide a more precise representation of a quantity than decimals, especially when dealing with irrational numbers that don't have exact decimal equivalents. Also, keeping the fractions can sometimes simplify calculations, particularly when working with certain types of equations or identities.
Methods for Eliminating Fractions
Now let's explore the various techniques used to eliminate fractions:
1. Finding a Common Denominator (for addition and subtraction)
When adding or subtracting fractions, the first step is to find a common denominator. This is a number that is a multiple of all the denominators involved. Once you have a common denominator, you can rewrite each fraction with the common denominator and then add or subtract the numerators. For example:
1/2 + 1/3 = (3/6) + (2/6) = 5/6
2. Multiplying by the Reciprocal (for division)
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. To divide by a fraction, multiply by its reciprocal.
1/2 ÷ 2/3 = 1/2 * 3/2 = 3/4
3. Clearing Fractions in Equations (using the Least Common Multiple - LCM)
This is a powerful technique for solving algebraic equations containing fractions. The key is to identify the least common multiple (LCM) of all the denominators in the equation. Then, multiply both sides of the equation by the LCM. This will effectively clear all the fractions from the equation.
Example:
Solve for x: x/2 + x/3 = 5
-
Find the LCM: The LCM of 2 and 3 is 6.
-
Multiply both sides by the LCM: 6(x/2 + x/3) = 6 * 5
-
Simplify: 3x + 2x = 30
-
Solve for x: 5x = 30 => x = 6
4. Converting Fractions to Decimals
Sometimes, the easiest way to get rid of fractions is simply to convert them into their decimal equivalents. This is particularly useful when working with calculators or when dealing with situations where decimal representation is more convenient. Simply divide the numerator by the denominator to get the decimal equivalent.
For example: 1/2 = 0.5 and 3/4 = 0.75
5. Simplifying Fractions Before Operations
Before performing any operation with fractions, it's always a good idea to simplify them first. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. This reduces the size of the numbers and simplifies calculations. For example:
6/8 simplifies to 3/4 (by dividing both numerator and denominator by 2).
Advanced Techniques for Eliminating Fractions
For more complex scenarios, especially in advanced algebra and calculus, more sophisticated techniques are often necessary.
Working with Complex Fractions
A complex fraction is a fraction where the numerator, denominator, or both contain fractions. To simplify these, often a combination of the previously mentioned techniques is required. One common strategy is to find a common denominator for all the fractions within the complex fraction and then simplify.
Solving Equations with Fractions and Variables in the Denominator
Equations with variables in the denominator require extra caution. The first step is to identify any values of the variable that would make the denominator zero. These values are called restrictions and must be excluded from the solution set. Then, the equation can be solved using the LCM method, keeping in mind the restrictions.
Dealing with Fractions in Inequalities
The process for solving inequalities with fractions is similar to that of equations. The main difference is that you must be careful to consider the direction of the inequality symbol when multiplying or dividing by a negative number. If you multiply or divide by a negative number, the inequality symbol must be flipped.
Practical Applications: Real-World Examples
The ability to eliminate fractions is crucial in a wide range of applications:
-
Baking: Recipes often use fractions to specify ingredient amounts. Eliminating fractions allows for precise measurements.
-
Construction and Engineering: In construction and engineering, precise calculations are paramount. Eliminating fractions improves accuracy in designs and measurements.
-
Finance: Calculating interest, profits, and losses often involves fractions. Converting them to decimals can simplify these calculations.
-
Computer Programming: Fractions are sometimes used in algorithms and calculations in programming. Eliminating fractions can lead to more efficient code.
Conclusion: Mastering Fraction Manipulation
Mastering the art of eliminating fractions is a valuable skill with wide-ranging applications. Whether you're tackling a simple arithmetic problem or solving a complex algebraic equation, understanding the various techniques for dealing with fractions will significantly improve your mathematical skills and problem-solving abilities. Remember to choose the most appropriate method based on the specific problem you're facing and always double-check your work to ensure accuracy. By practicing regularly and employing the strategies discussed in this guide, you can confidently conquer fractions and unlock your full mathematical potential. Happy calculating!
Latest Posts
Latest Posts
-
Is Boiling Water Physical Or Chemical Change
Apr 06, 2025
-
2x Y 1 In Slope Intercept Form
Apr 06, 2025
-
What Percentage Is 25 Of 60
Apr 06, 2025
-
Identify The Change Of State Occurring In Each Situation
Apr 06, 2025
-
What Is The Coefficient Of In The Expansion Of
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How To Get Rid Of Fractions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
