How To Find Radius From Arc Length
listenit
Mar 25, 2025 · 5 min read
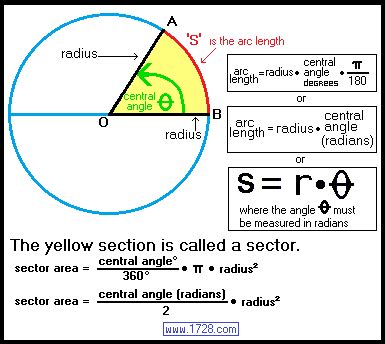
Table of Contents
How to Find the Radius from Arc Length: A Comprehensive Guide
Determining the radius of a circle given its arc length is a fundamental concept in geometry and trigonometry with wide applications in various fields, from engineering and architecture to computer graphics and surveying. This comprehensive guide will explore multiple methods to calculate the radius, catering to different levels of mathematical understanding and problem complexity. We'll cover the basic formula, address scenarios involving central angles, and delve into more advanced situations.
Understanding the Fundamentals: Arc Length, Radius, and Central Angle
Before jumping into the calculations, let's establish a clear understanding of the key elements involved:
-
Radius (r): The distance from the center of a circle to any point on its circumference. This is the value we're aiming to find.
-
Arc Length (s): The distance along the curved boundary of a circle between two points. This is a given value in our problems.
-
Central Angle (θ): The angle subtended by the arc at the center of the circle. This angle is measured in radians or degrees. The relationship between radians and degrees is crucial: 180 degrees = π radians.
The Basic Formula: Connecting Arc Length, Radius, and Central Angle
The fundamental relationship between arc length, radius, and central angle is given by the equation:
s = rθ
Where:
- s represents the arc length
- r represents the radius
- θ represents the central angle in radians.
This formula provides the cornerstone for calculating the radius if we know the arc length and the central angle. Remember, θ must be in radians for this formula to be accurate.
Example 1: Calculating the Radius with Known Arc Length and Central Angle (Radians)
Let's say we have an arc length of 10 cm and a central angle of 2 radians. We can rearrange the formula to solve for the radius:
r = s/θ = 10 cm / 2 radians = 5 cm
The radius of the circle is 5 cm.
Example 2: Calculating the Radius with Known Arc Length and Central Angle (Degrees)
If the central angle is given in degrees, we must first convert it to radians using the conversion factor:
Radians = (Degrees × π) / 180
Let's assume we have an arc length of 15 cm and a central angle of 60 degrees. First, convert the angle to radians:
Radians = (60 × π) / 180 = π/3 radians
Now, we can calculate the radius:
r = s/θ = 15 cm / (π/3 radians) ≈ 14.32 cm
The radius of the circle is approximately 14.32 cm.
Advanced Scenarios and Problem Solving Techniques
While the basic formula provides a straightforward solution in many cases, real-world applications often present more complex scenarios. Let's explore some of them:
Scenario 1: Finding the Radius when only Arc Length and a Portion of the Circle's Circumference are Known
Sometimes, instead of the central angle, we know the ratio of the arc length to the entire circumference. For instance, we might know that the arc represents one-quarter of the circle's circumference.
In this case, we can use the following approach:
-
Determine the central angle: If the arc represents a fraction f of the circumference, then the central angle is f * 2π radians (or f * 360 degrees).
-
Apply the basic formula: Use the calculated central angle and the given arc length in the formula
r = s/θto find the radius.
Example: An arc length of 8 cm represents 1/3 of the circle's circumference. This means the central angle is (1/3) * 2π = (2π/3) radians. The radius is:
r = s/θ = 8 cm / (2π/3 radians) ≈ 3.82 cm
Scenario 2: Utilizing Trigonometric Functions for Radius Calculation
In certain geometric problems, we might not have the central angle directly but have other information such as the length of a chord subtending the arc or the distance from the midpoint of the chord to the arc. In these cases, trigonometric functions become essential.
Example: Suppose we have an arc length of 12 cm and the length of the chord subtending the arc is 10 cm. Let's assume the distance from the midpoint of the chord to the center of the circle (also known as the apothem) is 'a'. This forms a right-angled triangle with half the chord length and the radius.
We can use trigonometric functions to solve for the radius indirectly. However, this approach requires more advanced geometric knowledge and may necessitate iterative numerical methods depending on the available information. We can establish relationships using the law of cosines and other trigonometric identities, but the solution often necessitates the use of calculators or computational tools.
Scenario 3: Dealing with Sectors and Segments
The calculation becomes slightly more involved when dealing with sectors (the area enclosed by two radii and the arc) or segments (the area enclosed by a chord and the arc). In these cases, additional formulae involving area calculations and trigonometric functions might be necessary to find the radius indirectly.
Practical Applications: Where Radius Calculation is Crucial
The ability to determine the radius from arc length has numerous practical applications across various disciplines:
-
Engineering: Designing curved structures like roads, railways, and bridges requires precise radius calculations to ensure stability and safety.
-
Architecture: Creating circular or arched elements in buildings necessitates accurate radius determination for aesthetically pleasing and structurally sound designs.
-
Surveying: Measuring the curvature of land and calculating distances using arc segments often involves calculating the radius.
-
Computer Graphics: Generating and manipulating curved shapes in computer graphics and animation relies heavily on accurate radius calculations.
-
Robotics: Path planning and movement control in robotics often involve working with circular paths and arc segments, which requires radius computation.
-
Astronomy: Analyzing celestial trajectories and orbits often involves calculating radii of curved paths.
Conclusion: Mastering Radius Calculation for Diverse Applications
Determining the radius of a circle from its arc length is a fundamental skill with far-reaching applications. While the basic formula offers a straightforward approach in many instances, understanding advanced scenarios and employing different problem-solving techniques is crucial for tackling more complex situations. This comprehensive guide provides a solid foundation for understanding and applying these calculations in diverse fields, whether you're an engineering student, an architect, a programmer, or simply curious about the fascinating world of geometry. Remember to always double-check your work and utilize appropriate tools and software when dealing with complex geometrical problems. The more you practice, the more proficient you will become in mastering this essential skill.
Latest Posts
Latest Posts
-
What Is 3 6 As A Fraction
Mar 28, 2025
-
How Many Cups In 1 2 Gal
Mar 28, 2025
-
39 Is What Percent Of 12 5
Mar 28, 2025
-
During Which Stage Of Cell Cycle Does Dna Replication Occur
Mar 28, 2025
-
What Is The Square Root Of Negative 2
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about How To Find Radius From Arc Length . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
