How To Find Area Of A Non Right Triangle
listenit
Mar 29, 2025 · 6 min read
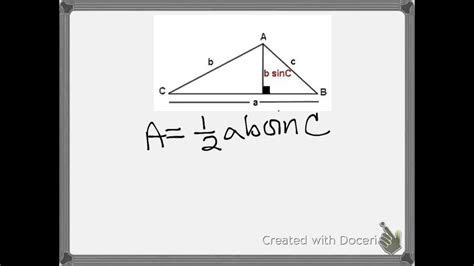
Table of Contents
How to Find the Area of a Non-Right Triangle: A Comprehensive Guide
Finding the area of a right-angled triangle is straightforward: it's half the base times the height. But what about non-right triangles? These triangles, lacking a convenient 90-degree angle, require different approaches. This comprehensive guide will explore several methods for calculating the area of non-right triangles, catering to various levels of mathematical understanding. We'll delve into the underlying principles and provide practical examples to solidify your grasp of these techniques.
Understanding the Fundamentals: Area and Triangles
Before diving into the methods, let's establish a fundamental understanding. The area of any triangle, regardless of its angles, is fundamentally defined as half the product of its base and its corresponding height. The key here is identifying the base and its corresponding height. The height is always the perpendicular distance from the base to the opposite vertex (corner).
This principle remains consistent across all triangle types, including obtuse (one angle greater than 90 degrees), acute (all angles less than 90 degrees), and scalene (all sides of different lengths). The challenge lies in determining the height when it's not directly given.
Method 1: Using Heron's Formula
Heron's formula is a powerful tool for finding the area of a triangle when you know the lengths of all three sides (a, b, c). It's particularly useful when the height isn't readily available.
1. Calculate the semi-perimeter (s):
The semi-perimeter is half the sum of the three sides: s = (a + b + c) / 2
2. Apply Heron's Formula:
The area (A) is calculated using the following formula:
A = √[s(s - a)(s - b)(s - c)]
Example:
Let's say we have a triangle with sides a = 5 cm, b = 6 cm, and c = 7 cm.
-
Calculate the semi-perimeter (s): s = (5 + 6 + 7) / 2 = 9 cm
-
Apply Heron's Formula:
A = √[9(9 - 5)(9 - 6)(9 - 7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
Therefore, the area of the triangle is approximately 14.7 square centimeters.
Advantages of Heron's Formula:
- Requires only side lengths: This makes it versatile when height information is unavailable.
- Works for all triangles: It's applicable to acute, obtuse, and scalene triangles.
Disadvantages of Heron's Formula:
- Can be computationally intensive: Especially for triangles with large side lengths or irrational numbers.
Method 2: Using Trigonometry: The Sine Rule
Trigonometry provides an elegant way to calculate the area when you know two sides and the included angle. This method utilizes the sine function.
1. Identify the known values:
You need the lengths of two sides (a and b) and the angle (C) between them.
2. Apply the formula:
The area (A) is given by:
A = (1/2)ab sin(C)
Example:
Consider a triangle with sides a = 8 cm, b = 10 cm, and the included angle C = 30°.
-
Apply the formula:
A = (1/2) * 8 * 10 * sin(30°) = 40 * 0.5 = 20 cm²
Therefore, the area of the triangle is 20 square centimeters.
Advantages of the Sine Rule:
- Relatively simple calculation: Easier than Heron's formula for some scenarios.
- Direct application of known values: Requires fewer intermediate steps.
Disadvantages of the Sine Rule:
- Requires specific information: You must know two sides and the included angle.
Method 3: Coordinate Geometry Approach
If the vertices of the triangle are defined by their coordinates on a Cartesian plane (x, y), we can employ the determinant method to calculate the area. This is particularly useful when dealing with triangles in computer graphics or other computational contexts.
1. Define the coordinates:
Let the vertices be A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃).
2. Apply the determinant formula:
The area (A) is given by:
A = (1/2) |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)| The absolute value ensures a positive area.
Example:
Let's say the vertices are A(1, 2), B(4, 6), and C(7, 3).
-
Apply the determinant formula:
A = (1/2) |1(6 - 3) + 4(3 - 2) + 7(2 - 6)| = (1/2) |3 + 4 - 28| = (1/2) |-21| = 10.5 square units.
Advantages of the Coordinate Geometry Approach:
- Useful for computer graphics and computational applications: Easily implemented in algorithms.
- Works for any triangle: Applicable to all types of triangles.
Disadvantages of the Coordinate Geometry Approach:
- Requires coordinate information: Not applicable if coordinates are unknown.
- Can be tedious for manual calculation: Prone to errors if not carefully calculated.
Method 4: Dividing into Right Triangles
This is a geometric approach where you divide the non-right triangle into two or more right-angled triangles. This allows you to use the standard right triangle area formula (1/2 * base * height) for each sub-triangle and then sum the areas to find the total area of the original non-right triangle.
1. Identify the altitude (height): Determine the height of the triangle, drawing a perpendicular line from one vertex to the opposite side. This line creates two right-angled triangles.
2. Calculate the areas of the right triangles: Use the formula (1/2 * base * height) for each right-angled triangle.
3. Sum the areas: Add the areas of the individual right-angled triangles to obtain the area of the original non-right triangle.
Example: Let's say you have a triangle with a base of 10 units and a height of 6 units, and the altitude divides the base into segments of 4 and 6 units.
-
Triangle 1: (1/2) * 4 * 6 = 12 square units
-
Triangle 2: (1/2) * 6 * 6 = 18 square units
-
Total Area: 12 + 18 = 30 square units
Advantages of the Dividing into Right Triangles Method:
- Intuitive and visually clear: Easy to understand the process.
- Applicable to a wide range of triangles: Especially useful when you can easily identify right triangles within the larger triangle.
Disadvantages of the Dividing into Right Triangles Method:
- Requires careful geometric construction: You might need to use additional geometric tools.
- Not always straightforward: The construction of right triangles might not always be easily achievable or might lead to complex calculations.
Choosing the Right Method
The best method for calculating the area of a non-right triangle depends on the information available.
- Heron's formula: Ideal when you only know the lengths of all three sides.
- Trigonometry (Sine Rule): Best when you know two sides and the included angle.
- Coordinate Geometry: Most suitable when you have the coordinates of the vertices.
- Dividing into Right Triangles: Useful when visualizing the triangle and its decomposition into right triangles makes calculations simpler.
By understanding these methods and their respective advantages and disadvantages, you'll be well-equipped to tackle a wide variety of triangle area problems with confidence. Remember to always double-check your calculations to ensure accuracy. Mastering these techniques will enhance your problem-solving skills and solidify your understanding of geometric principles.
Latest Posts
Latest Posts
-
What Is 1000 Feet In Miles
Apr 01, 2025
-
Atomic Mass Of H2 S O4
Apr 01, 2025
-
How Many Neutrons Does Chromium Have
Apr 01, 2025
-
What Is The Element With The Highest Electronegativity Value
Apr 01, 2025
-
12 Of 50 Is What Number
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Find Area Of A Non Right Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
