How To Convert Polar Equations To Rectangular Form
listenit
Mar 26, 2025 · 6 min read
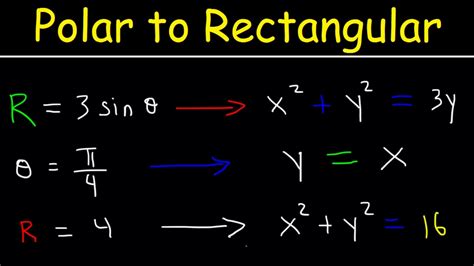
Table of Contents
How to Convert Polar Equations to Rectangular Form: A Comprehensive Guide
Converting polar equations to rectangular form is a fundamental skill in mathematics, particularly in analytic geometry and calculus. Understanding this process allows you to visualize and manipulate equations more easily, opening up possibilities for graphing, analysis, and problem-solving. This comprehensive guide will delve into the intricacies of this conversion, providing you with a step-by-step approach, numerous examples, and insightful tips for mastering this essential technique.
Understanding Polar and Rectangular Coordinate Systems
Before diving into the conversion process, let's refresh our understanding of the two coordinate systems involved.
Rectangular Coordinates (Cartesian Coordinates)
The rectangular coordinate system, also known as the Cartesian coordinate system, uses two perpendicular axes, the x-axis and the y-axis, to locate points in a plane. A point is represented by an ordered pair (x, y), where x represents the horizontal distance from the origin and y represents the vertical distance from the origin.
Polar Coordinates
The polar coordinate system uses a distance and an angle to locate points in a plane. A point is represented by an ordered pair (r, θ), where:
- r: Represents the distance from the origin (also called the pole) to the point. This distance is always non-negative (r ≥ 0).
- θ: Represents the angle (in radians or degrees) measured counterclockwise from the positive x-axis to the line segment connecting the origin to the point.
The Fundamental Conversion Equations
The key to converting between polar and rectangular coordinates lies in the relationships between these two systems. These relationships are derived from basic trigonometry:
- x = r cos θ
- y = r sin θ
- r² = x² + y²
- tan θ = y/x (Note: This equation has limitations; we'll discuss these later.)
These four equations are the cornerstones of our conversion process. Let's explore how to use them effectively.
Converting Polar Equations to Rectangular Form: A Step-by-Step Approach
The process of converting a polar equation to rectangular form involves strategically substituting the rectangular equivalents for the polar terms (r and θ) using the equations above. The specific steps may vary depending on the complexity of the polar equation. However, a general approach involves:
-
Identify the polar terms (r and θ) in the equation.
-
Substitute the appropriate rectangular equivalents. This usually involves using
x = r cos θ,y = r sin θ, andr² = x² + y². The choice of substitution depends on the structure of the equation. Sometimes, manipulating the equation algebraically before substituting is beneficial. -
Simplify the resulting equation. Use algebraic manipulation to simplify the equation into a standard rectangular form. This might involve expanding terms, factoring, or completing the square.
-
Verify the result (optional). While not always necessary, verifying your result by checking a few points can help catch errors. Plot a few points in the polar coordinate system using the original equation, then convert those points to rectangular coordinates and check if they satisfy the converted equation.
Examples: Illustrating the Conversion Process
Let's work through several examples to illustrate the conversion process and highlight various techniques.
Example 1: A Simple Equation
Convert the polar equation r = 5 to rectangular form.
- Step 1: Identify polar terms: r is the only polar term.
- Step 2: Substitute: We use
r² = x² + y². Since r = 5, r² = 25. Therefore, we havex² + y² = 25. - Step 3: Simplify: The equation is already simplified. This represents a circle with a radius of 5 centered at the origin.
Example 2: Incorporating θ
Convert the polar equation r = 2 cos θ to rectangular form.
- Step 1: Identify polar terms: r and θ.
- Step 2: Substitute: Multiply both sides by r: r² = 2r cos θ. Then substitute
r² = x² + y²andx = r cos θ. This givesx² + y² = 2x. - Step 3: Simplify: Rearrange the equation to get
x² - 2x + y² = 0. Complete the square for x:(x - 1)² - 1 + y² = 0, which simplifies to(x - 1)² + y² = 1. This represents a circle with a radius of 1 centered at (1, 0).
Example 3: A More Complex Equation
Convert the polar equation r = 1 + cos θ to rectangular form.
-
Step 1: Identify polar terms: r and θ.
-
Step 2: Substitute: Multiply both sides by r: r² = r + r cos θ. Substitute
r² = x² + y²,x = r cos θ, and solve for r: r = x² + y² - x. Now substitute this intox = r cos θ: x = (x² + y² - x)cos θ. This doesn’t directly lead to a simple substitution. Instead, let’s try a different approach. Start by multiplying by r: r² = r + r cos θ. Then substitute: x² + y² = r + x. Now, solve for r: r = x² + y² - x. Substitute this into r² = x² + y². (x² + y²) = (x² + y² - x)² -
Step 3: Simplify: This leads to a complicated equation, requiring more advanced algebraic manipulation. This highlights that some conversions may require careful consideration of different substitution strategies and algebraic manipulation techniques. The simplified form is often a complex curve.
Example 4: Handling tan θ
Convert the polar equation θ = π/4 to rectangular form.
- Step 1: Identify polar terms: θ.
- Step 2: Substitute: Use
tan θ = y/x. Since θ = π/4, tan(π/4) = 1. Therefore, y/x = 1. - Step 3: Simplify: y = x. This represents a straight line passing through the origin with a slope of 1.
Handling Special Cases and Limitations
The equation tan θ = y/x has a crucial limitation: it's undefined when x = 0. This means it cannot be used directly when the line passes through the origin. In these situations, you'll need to consider the geometry of the problem or use a different approach based on the specifics of the equation.
Additionally, remember that r is always non-negative. Therefore, any resulting rectangular equation should reflect this constraint, either implicitly or explicitly.
Advanced Techniques and Applications
For more complex polar equations, you might need to employ advanced algebraic techniques like completing the square, factoring, or using trigonometric identities to simplify the resulting rectangular equations. These techniques are crucial for expressing the converted equations in their most recognizable and usable forms.
Conclusion: Mastering the Conversion Process
Converting polar equations to rectangular form is a valuable skill with applications in various mathematical fields. By understanding the fundamental conversion equations, employing a systematic approach, and practicing with diverse examples, you can confidently navigate this important aspect of analytic geometry. Remember that patience and careful algebraic manipulation are key to success in this process. The more you practice, the more adept you will become at recognizing the most efficient substitution strategies and simplifying the resulting equations. Mastering this skill will significantly enhance your ability to visualize, analyze, and manipulate geometric relationships effectively.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 28 And 42
Mar 26, 2025
-
Does Nitrogen Follow The Octet Rule
Mar 26, 2025
-
Is 37 A Prime Number Or A Composite Number
Mar 26, 2025
-
21 Out Of 30 Is What Percent
Mar 26, 2025
-
Cos 4x Sin 4x Cos 2x
Mar 26, 2025
Related Post
Thank you for visiting our website which covers about How To Convert Polar Equations To Rectangular Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
