How Many Right Angles Does Rectangle Have
listenit
Apr 05, 2025 · 6 min read
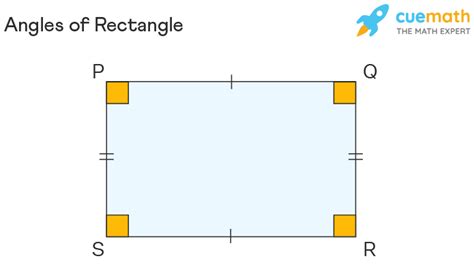
Table of Contents
How Many Right Angles Does a Rectangle Have? A Deep Dive into Geometry
Understanding the properties of shapes is fundamental to geometry. One of the most basic, yet crucial, shapes is the rectangle. While many might immediately know the answer to the question "How many right angles does a rectangle have?", a deeper exploration reveals fascinating connections to other geometric concepts and their practical applications. This article delves into the intricacies of rectangles, exploring not only the number of right angles but also their defining characteristics and significance in various fields.
Defining a Rectangle: More Than Just Four Right Angles
A rectangle, in its simplest definition, is a quadrilateral – a four-sided polygon – with four right angles. This seemingly straightforward definition actually encapsulates a wealth of geometrical properties. Let's break down the key elements:
- Quadrilateral: This specifies the number of sides: four. It's a crucial starting point, distinguishing a rectangle from triangles or other polygons.
- Four Right Angles: This is the defining characteristic of a rectangle. A right angle, measured as 90 degrees, is formed where two perpendicular lines intersect. This is the feature that sets a rectangle apart from other quadrilaterals like parallelograms or trapezoids.
The Significance of Right Angles
The presence of four right angles in a rectangle has profound consequences:
- Parallel Sides: Because of the right angles, opposite sides of a rectangle are parallel to each other. This parallelism is a direct consequence of the angles and leads to further properties.
- Equal Opposite Sides: Again, due to the right angles and the inherent parallelism, opposite sides of a rectangle are equal in length. This property is crucial in various calculations and applications.
- Diagonals Bisect Each Other: The diagonals of a rectangle (lines connecting opposite corners) intersect at their midpoints, dividing each other into two equal segments. This property provides useful tools for geometrical constructions and proofs.
Beyond the Basics: Rectangles and Related Shapes
Understanding the properties of a rectangle allows us to explore its relationship with other geometric shapes. Rectangles belong to a broader family of quadrilaterals:
- Parallelograms: All rectangles are parallelograms, meaning they have two pairs of parallel sides. However, not all parallelograms are rectangles (a parallelogram doesn't necessarily have right angles).
- Squares: A square is a special type of rectangle. It possesses all the properties of a rectangle (four right angles, parallel and equal opposite sides) but adds an additional constraint: all four sides are equal in length. This makes the square a highly symmetrical shape.
This hierarchical relationship highlights the importance of understanding the defining characteristics of each shape. Recognizing that a rectangle is a specific type of parallelogram, for instance, allows for efficient problem-solving and clearer categorization of shapes.
Real-World Applications: Rectangles Everywhere
The ubiquity of rectangles in our daily lives underscores their importance. From the screens we use to the buildings we inhabit, rectangles are fundamental to our built environment and technology.
- Architecture and Construction: Buildings, rooms, windows, and doors are often rectangular. This shape offers structural stability and efficient use of space.
- Digital Design: Computer screens, images, and documents are almost universally rectangular. This format is well-suited to digital display and data organization.
- Packaging and Manufacturing: Boxes, containers, and many manufactured products are rectangular due to their ease of stacking, transportation, and storage.
- Everyday Objects: Many everyday objects, from books and photographs to tables and tiles, are rectangular in shape.
These examples demonstrate the practical relevance of understanding rectangular geometry. The properties of rectangles dictate design choices, manufacturing processes, and the overall functionality of numerous everyday items.
Mathematical Exploration: Area, Perimeter, and Diagonals
The simple yet powerful properties of a rectangle allow us to derive formulas for calculating its area, perimeter, and diagonal length:
- Area: The area of a rectangle is calculated by multiplying its length and width: Area = Length x Width. This formula is fundamental in calculating surface areas and volumes of various three-dimensional objects.
- Perimeter: The perimeter, or the total distance around the rectangle, is calculated by adding the lengths of all four sides: Perimeter = 2(Length + Width). This is crucial for determining the amount of material needed to create a rectangular structure or enclosure.
- Diagonal Length: Using the Pythagorean theorem, we can calculate the length of a rectangle's diagonal: Diagonal² = Length² + Width². This is useful in a variety of geometrical problems and constructions.
These formulas demonstrate the practical application of rectangular geometry in problem-solving and quantitative analysis. The ability to calculate these values is essential in numerous engineering, architectural, and design applications.
Advanced Concepts: Rectangles in Higher Dimensions
While the standard definition of a rectangle focuses on two dimensions, the concept extends to higher dimensions. A three-dimensional rectangular prism (often called a cuboid) has six rectangular faces, twelve edges, and eight vertices. The principles of parallelism, right angles, and equal opposite sides extend to these higher-dimensional shapes. This concept finds relevance in fields like computer graphics, where 3D models are commonly represented using rectangular prisms as building blocks.
Furthermore, the mathematical properties of rectangles in lower dimensions serve as the foundation for understanding similar concepts in higher dimensions. The understanding gained from analyzing a simple rectangle in 2D provides a solid base for exploring more complex geometric structures in higher dimensional spaces.
Rectangles and Tessellations: Covering a Plane
Rectangles possess a unique property: they can tessellate. Tessellation refers to the ability of a shape to cover a plane without any gaps or overlaps. This is because the angles of a rectangle add up to 360 degrees, allowing them to fit perfectly together without leaving any spaces. This property is widely used in art, design, and architecture to create repeating patterns and covering surfaces efficiently. The ability of rectangles to tessellate demonstrates their geometrical elegance and practical implications in design and construction.
Error Analysis: Common Misconceptions about Rectangles
While the concept of a rectangle seems straightforward, some common misconceptions can arise:
- Confusing Rectangles with Squares: While a square is a specific type of rectangle, not all rectangles are squares. It's important to remember that the equal side lengths are a distinguishing feature of the square, a subset of the rectangles.
- Assuming All Quadrilaterals are Rectangles: Not all four-sided shapes are rectangles. Parallelograms, trapezoids, and rhombuses are other types of quadrilaterals with different properties.
- Incorrect Calculations: Errors can occur when calculating the area, perimeter, or diagonal length, especially when dealing with units or conversions. Careful attention to detail is crucial for accuracy.
Addressing these misconceptions ensures a clear and accurate understanding of rectangular properties and their applications.
Conclusion: The Enduring Importance of Rectangles
In conclusion, the simple question of how many right angles a rectangle has—four—opens a gateway to a rich understanding of geometry. The properties of rectangles are not just abstract mathematical concepts; they underpin countless aspects of our daily lives, from the architecture of our buildings to the design of our technology. By understanding these properties, we can appreciate the profound impact of this seemingly simple shape on the world around us. The exploration of rectangles extends beyond its basic definition, reaching into advanced mathematical concepts and demonstrating the elegance and utility of geometric principles. This multifaceted nature of the rectangle highlights its enduring importance in both theoretical mathematics and practical applications.
Latest Posts
Latest Posts
-
3 5 Divided By 2 As A Fraction
Apr 06, 2025
-
How Far Is A Hundred Meters
Apr 06, 2025
-
What Is The Circumference Of An 8 Inch Circle
Apr 06, 2025
-
What Is The Absolute Value Of 3
Apr 06, 2025
-
Lcm Of 5 8 And 12
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How Many Right Angles Does Rectangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
