Lcm Of 5 8 And 12
listenit
Apr 06, 2025 · 5 min read
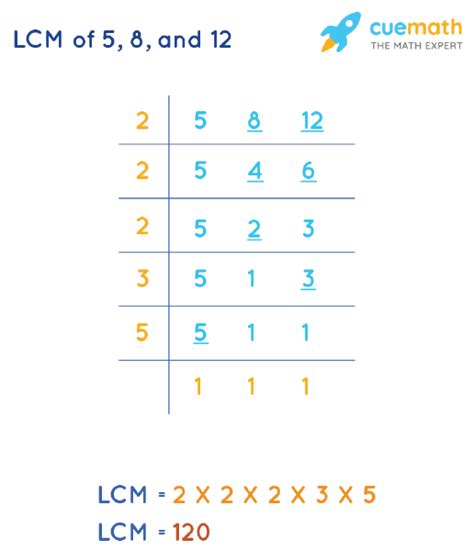
Table of Contents
Finding the Least Common Multiple (LCM) of 5, 8, and 12: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and number theory. Understanding how to find the LCM is essential for solving various mathematical problems. This comprehensive guide will explore different methods for calculating the LCM of 5, 8, and 12, providing a step-by-step breakdown and explaining the underlying principles. We'll delve into the significance of LCM in real-world applications and offer valuable tips for efficient calculation.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's solidify our understanding of LCM. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Key Characteristics of LCM:
- Smallest Multiple: The LCM is always the smallest among all the common multiples of the given numbers.
- Divisibility: The LCM is perfectly divisible (leaves no remainder) by each of the original numbers.
- Applications: LCM finds applications in various scenarios, from simplifying fractions to scheduling events with recurring intervals.
Methods for Finding the LCM of 5, 8, and 12
We will explore three common methods for calculating the LCM:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, ...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
By comparing the lists, we can identify the smallest common multiple: 120.
Advantages: Simple and intuitive, easily understandable for beginners.
Disadvantages: Inefficient for larger numbers; listing multiples can become time-consuming and tedious.
2. Prime Factorization Method
This method is more efficient, especially when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime Factorization of 5: 5 (5 is a prime number)
- Prime Factorization of 8: 2³ (8 = 2 x 2 x 2)
- Prime Factorization of 12: 2² x 3 (12 = 2 x 2 x 3)
Now, we identify the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
To find the LCM, we multiply these highest powers together: 2³ x 3 x 5 = 8 x 3 x 5 = 120
Advantages: Efficient for larger numbers, systematic approach.
Disadvantages: Requires knowledge of prime factorization.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between LCM and GCD (Greatest Common Divisor). The product of the LCM and GCD of two or more numbers is equal to the product of the numbers themselves.
First, let's find the GCD of 5, 8, and 12 using the Euclidean algorithm or prime factorization. Since 5 is a prime number and 8 and 12 do not share any common factors with 5, the GCD of 5, 8, and 12 is 1.
Let's denote:
- a = 5
- b = 8
- c = 12
We know that LCM(a, b, c) * GCD(a, b, c) = a * b * c
Therefore, LCM(5, 8, 12) = (5 * 8 * 12) / GCD(5, 8, 12) = (480) / 1 = 120
Advantages: Relatively efficient, leverages the relationship between LCM and GCD.
Disadvantages: Requires understanding of GCD calculation.
Real-World Applications of LCM
The concept of LCM extends beyond theoretical mathematics, finding practical applications in various real-world scenarios:
-
Scheduling Events: Imagine you have three events that repeat at intervals of 5, 8, and 12 days. The LCM helps determine when all three events will coincide again. In this case, it would be 120 days.
-
Fraction Operations: When adding or subtracting fractions, finding the LCM of the denominators is crucial for obtaining a common denominator, simplifying the calculation.
-
Gear Ratios: In mechanical engineering, LCM is used in determining gear ratios and calculating the speeds of rotating components.
-
Music Theory: The concept of LCM is applicable in music theory, particularly in determining the rhythmic patterns and harmonies.
-
Project Management: Scheduling tasks with recurring dependencies often involves utilizing LCM to synchronize activities effectively.
Tips for Efficient LCM Calculation
-
Start with Prime Factorization: For larger numbers, prime factorization is the most efficient method.
-
Utilize Online Calculators: Many online calculators can compute LCM quickly and accurately, particularly helpful for complex calculations.
-
Understand the Relationships: Knowing the relationship between LCM and GCD can streamline calculations.
-
Practice Regularly: Consistent practice solidifies understanding and enhances calculation speed.
Conclusion
Finding the LCM of 5, 8, and 12, whether through listing multiples, prime factorization, or the GCD method, ultimately yields the same result: 120. Understanding the different methods allows you to choose the most appropriate approach depending on the complexity of the numbers involved. The significance of LCM extends far beyond classroom exercises, finding practical application in numerous real-world scenarios. By mastering the concepts and techniques presented in this guide, you'll be well-equipped to tackle LCM problems with confidence and efficiency. Remember to practice regularly to solidify your understanding and improve your problem-solving skills. The ability to calculate LCM effectively is a valuable asset in various mathematical and practical applications.
Latest Posts
Latest Posts
-
How Many Minutes Are In 40 Miles
Apr 06, 2025
-
What Is The Value Of 3 4
Apr 06, 2025
-
Is Sodium Solid Liquid Or Gas
Apr 06, 2025
-
What Units Are Used To Measure Power
Apr 06, 2025
-
Empirical Formula Of Copper Ii Oxide
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
