How Many Lines Of Symmetry Rectangle
listenit
Mar 26, 2025 · 6 min read
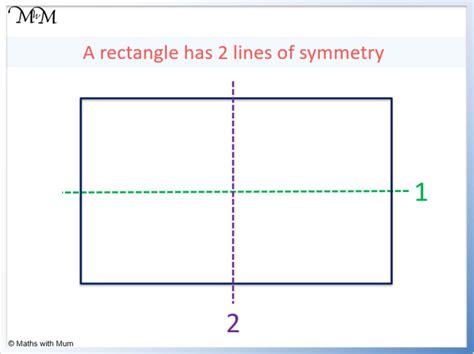
Table of Contents
How Many Lines of Symmetry Does a Rectangle Have? A Deep Dive into Geometric Symmetry
Symmetry, a fundamental concept in mathematics and geometry, plays a crucial role in understanding the properties of shapes. This article delves into the fascinating world of symmetry, focusing specifically on the number of lines of symmetry a rectangle possesses. We'll explore the definition of symmetry, different types of symmetry, and then meticulously analyze the case of rectangles, clarifying any misconceptions along the way. This comprehensive guide will equip you with a thorough understanding of rectangular symmetry, useful for students, educators, and anyone interested in geometry.
Understanding Lines of Symmetry
Before we tackle rectangles, let's define what we mean by a line of symmetry. A line of symmetry, also known as a line of reflection, is a line that divides a shape into two identical halves that are mirror images of each other. Imagine folding the shape along this line – both halves would perfectly overlap. A shape can have multiple lines of symmetry, zero lines of symmetry, or just one. The number of lines of symmetry is a key characteristic that distinguishes different geometric shapes.
Types of Symmetry
Beyond lines of symmetry, it's important to acknowledge other types of symmetry:
- Reflectional Symmetry (Bilateral Symmetry): This is the type of symmetry we are primarily focusing on here. It involves reflecting a shape across a line to produce a mirror image. This is the symmetry defined by lines of symmetry.
- Rotational Symmetry: A shape possesses rotational symmetry if it can be rotated less than 360 degrees about a central point and still look identical to its original position. The order of rotational symmetry indicates how many times it looks identical during a 360-degree rotation.
- Translational Symmetry: This type of symmetry is found in repeating patterns where the shape is repeatedly translated (moved) without any rotation or reflection.
Exploring Rectangular Symmetry
Now, let's focus our attention on rectangles. A rectangle is a quadrilateral (four-sided polygon) with four right angles. Its opposite sides are parallel and equal in length. The key question is: how many lines of symmetry does a rectangle possess?
The answer, which might surprise some, is two.
Let's visualize this:
-
Vertical Line of Symmetry: Imagine a vertical line drawn exactly down the middle of the rectangle, dividing it into two equal, mirror-image halves. Folding the rectangle along this line would perfectly overlap both halves.
-
Horizontal Line of Symmetry: Now imagine a horizontal line drawn exactly across the middle of the rectangle. Again, this line divides the rectangle into two identical mirror-image halves. Folding along this line would lead to a perfect overlap.
Therefore, a rectangle has two lines of symmetry: one vertical and one horizontal. It's crucial to understand that these lines must pass through the center of the rectangle to be considered lines of symmetry.
Why Not More? A Deeper Look at Symmetry Requirements
You might be tempted to think a rectangle could have diagonal lines of symmetry. However, this isn't the case. Let's examine why:
A diagonal line drawn across a rectangle divides it into two triangles. While these triangles have equal areas, they are not mirror images of each other. To be a line of symmetry, each half must be a reflection of the other, meaning they are congruent and can be superimposed by a reflection. This condition is not met by the triangles created by a diagonal line in a rectangle.
Consequently, only the vertical and horizontal lines passing through the center fulfill the criteria of a line of symmetry.
Special Case: The Square
It's important to differentiate between rectangles and squares. A square is a special type of rectangle where all four sides are equal in length. While a square is a rectangle, it possesses additional lines of symmetry.
A square possesses four lines of symmetry:
- Two lines of symmetry: The vertical and horizontal lines as in any rectangle.
- Two diagonal lines of symmetry: The diagonal lines connecting opposite corners of the square create lines of reflection, resulting in two additional lines of symmetry. The triangles formed by these diagonals are mirror images of each other, fulfilling the requirement for a line of symmetry.
Applications of Symmetry in Real Life
Understanding symmetry, and the specific lines of symmetry in shapes like rectangles, has practical applications in many fields:
- Architecture and Design: Symmetry is aesthetically pleasing and often used in building design, creating balanced and harmonious structures. Rectangular shapes with their two lines of symmetry are commonly found in architecture.
- Art and Graphics: Artists and graphic designers utilize symmetry to create visually appealing compositions. The concept of reflection and mirror images is fundamental to many artistic techniques.
- Nature: Symmetry is prevalent in nature, from the symmetrical wings of butterflies to the symmetrical branching patterns of trees. Understanding symmetry helps us appreciate the natural world’s beauty and patterns.
- Engineering: Symmetry is essential in engineering to ensure balance and stability in structures and mechanical designs. Symmetrical designs often lead to more efficient and robust systems.
Symmetry and Transformations: A Mathematical Perspective
Lines of symmetry are intimately linked to geometric transformations, particularly reflections. A reflection is a transformation that maps a point to its mirror image across a line. The lines of symmetry of a shape are precisely the lines about which reflection leaves the shape unchanged.
Studying symmetry through the lens of transformations provides a more rigorous and mathematical understanding of the concept. It allows for a deeper exploration of the properties of shapes and their relationships.
Misconceptions about Rectangular Symmetry
A common misconception is that any line dividing a rectangle into two equal areas is a line of symmetry. This is incorrect. Equal area division is a necessary but not sufficient condition for a line of symmetry. The crucial element is that the two halves must be mirror images of each other.
Conclusion: Mastering the Lines of Symmetry in Rectangles
This comprehensive exploration of rectangular symmetry clarifies the number of lines of symmetry a rectangle possesses: two. We've explored the definition of lines of symmetry, differentiated between types of symmetry, and dissected the specific case of rectangles, highlighting the crucial distinction between equal area division and true reflectional symmetry. By understanding these concepts, we gain a deeper appreciation for the beauty and mathematical elegance inherent in geometry. This knowledge is applicable in various fields, from art and design to engineering and architecture, demonstrating the practical significance of symmetry in our world. We've also addressed common misconceptions, further solidifying your understanding of this fundamental geometrical concept. This detailed explanation should provide a robust understanding of rectangular symmetry for anyone curious about this fascinating topic.
Latest Posts
Latest Posts
-
Standard Enthalpy Of Formation Of Ethanol
Mar 29, 2025
-
Do Parallelograms Have 4 Right Angles
Mar 29, 2025
-
Least Common Multiple Of 10 And 8
Mar 29, 2025
-
Name 3 Ways To Dissolve Something Faster
Mar 29, 2025
-
Charged Language In I Have A Dream
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
