Do Parallelograms Have 4 Right Angles
listenit
Mar 29, 2025 · 5 min read
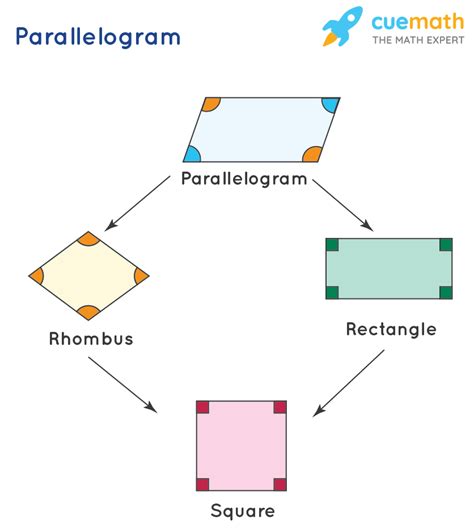
Table of Contents
Do Parallelograms Have 4 Right Angles? A Comprehensive Exploration of Quadrilateral Geometry
The question of whether parallelograms possess four right angles is a fundamental one in geometry, leading us into a fascinating exploration of quadrilateral properties. While the short answer is "not necessarily," understanding why requires a deeper dive into the defining characteristics of parallelograms and their relationship to other quadrilaterals, such as rectangles and squares. This article will comprehensively examine this question, clarifying the distinctions between different types of quadrilaterals and reinforcing key geometrical concepts.
Understanding Parallelograms: A Definition
A parallelogram is a quadrilateral (a four-sided polygon) with two pairs of parallel sides. This is the defining characteristic. It's crucial to remember that parallelism is the key differentiator. Parallel lines, by definition, never intersect, maintaining a constant distance between them. This simple definition unlocks several important properties of parallelograms:
Key Properties of Parallelograms:
- Opposite sides are equal in length: This means the lengths of opposite sides are congruent.
- Opposite angles are equal in measure: The angles directly opposite each other within the parallelogram are congruent.
- Consecutive angles are supplementary: Consecutive angles (angles next to each other) add up to 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at their midpoints.
It is essential to note that none of these properties inherently dictate that the angles are right angles. This is where the confusion often arises.
Differentiating Parallelograms from Rectangles and Squares
The confusion surrounding right angles in parallelograms often stems from a lack of clear distinction between parallelograms and their more specialized cousins: rectangles and squares.
Rectangles: Parallelograms with Right Angles
A rectangle is a special type of parallelogram where all four angles are right angles (90 degrees). Rectangles inherit all the properties of parallelograms, but the addition of right angles adds a crucial constraint. This means all the properties previously mentioned for parallelograms apply to rectangles, plus the property of having four right angles.
Squares: The Most Specialized Parallelogram
A square is an even more specialized quadrilateral. It's a rectangle with all sides equal in length. Therefore, a square is also a parallelogram, a rectangle, and a rhombus (a parallelogram with all sides equal). It inherits all the properties of parallelograms and rectangles, plus the additional constraint of having all sides of equal length.
Visualizing the Differences: A Diagrammatic Approach
Consider these diagrams:
A B
/ \ / \
/ \ / \
/ \ / \
D-------C D-------C
Parallelogram Rectangle
A B
/|\ /|\
/ | \ / | \
/ | \ / | \
D-------C D-------C
Square Rhombus (not a rectangle)
The first diagram shows a general parallelogram, where none of the angles are necessarily 90 degrees. The second shows a rectangle, where all angles are 90 degrees. The third illustrates a square, a special case of rectangle and rhombus with equal sides and right angles. The last shows a rhombus that is not a rectangle as it doesn't have 90-degree angles.
This visual representation clearly demonstrates that while all rectangles and squares are parallelograms, not all parallelograms are rectangles or squares.
Why Some Parallelograms Lack Right Angles: A Deeper Look at Geometry
The fundamental reason why not all parallelograms have four right angles lies in the definition itself. The definition only specifies that opposite sides are parallel. Parallelism does not imply perpendicularity (forming a right angle). Think of a leaning tower: the opposite sides might be parallel, but the angles are not 90 degrees. Similarly, a parallelogram can be skewed or tilted, maintaining parallel opposite sides without having right angles.
Real-World Examples: Parallelograms in Everyday Life
Parallelograms are abundant in everyday life, showcasing their various forms:
- Doors: Many doors, when open slightly, form a parallelogram.
- Windows: Some window frames can be parallelograms if they're not rectangular.
- Boxes: Boxes that are slightly skewed might resemble parallelograms if not viewed from the correct angle.
- Structures: Certain architectural structures may utilize parallelogram shapes for structural or aesthetic reasons.
Mathematical Proof and Counterexamples
While a formal mathematical proof to show that not all parallelograms are rectangles requires vector algebra or coordinate geometry, we can easily show a counterexample. Imagine drawing a parallelogram on a piece of paper. Now, shear it—push one side horizontally while maintaining the parallelism of opposite sides. The resulting shape is still a parallelogram, but its angles are no longer 90 degrees. This visual demonstration effectively refutes the idea that all parallelograms possess four right angles.
Common Misconceptions and Clarifications
Many misconceptions arise from the overlapping properties of parallelograms, rectangles, and squares. It’s crucial to understand that:
- Parallelogram is the most general term: It encompasses rectangles and squares, but not vice versa.
- Rectangles are specialized parallelograms: They add the constraint of right angles.
- Squares are the most specialized: They combine the properties of parallelograms and rectangles with equal sides.
Conclusion: Understanding the Nuances of Parallelogram Geometry
In conclusion, while parallelograms possess many valuable properties like opposite sides being equal and parallel, and opposite angles being equal, they do not necessarily have four right angles. This crucial distinction separates parallelograms from rectangles and squares, which are specialized subsets of parallelograms. Understanding these differences is crucial for a solid grasp of fundamental geometry and its application in various fields, from architecture to engineering. The key takeaway is that parallelism does not imply perpendicularity—a fundamental concept in understanding the distinctions within the family of quadrilaterals. Remember the defining characteristic: parallel opposite sides—and understand that this alone doesn't guarantee right angles.
Latest Posts
Latest Posts
-
What Percent Of 36 Is 45
Mar 31, 2025
-
14 Is 70 Of What Number
Mar 31, 2025
-
What Is Half Of 1 1 3 Cup In Cooking
Mar 31, 2025
-
3 And 1 2 As An Improper Fraction
Mar 31, 2025
-
What Is 60 Percent Of 200
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Do Parallelograms Have 4 Right Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
