How Many 1/4 Are In 2/3
listenit
May 25, 2025 · 5 min read
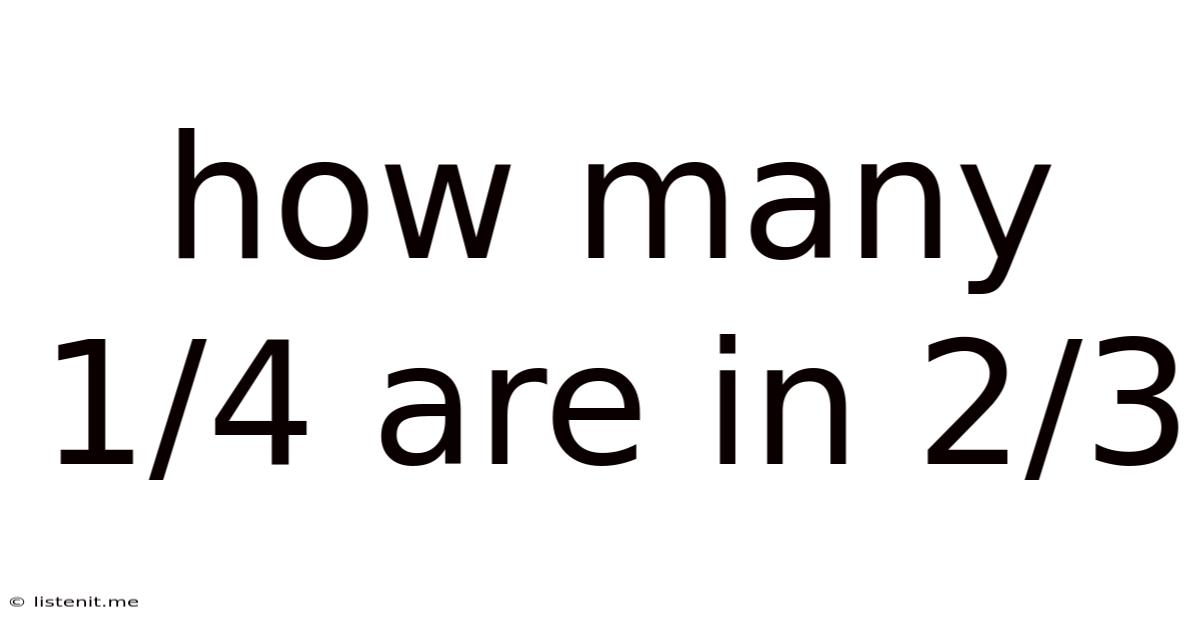
Table of Contents
How Many 1/4s are in 2/3? A Deep Dive into Fractions
This seemingly simple question, "How many 1/4s are in 2/3?", opens a door to a fascinating exploration of fractions, division, and mathematical reasoning. While a quick calculation might suffice for some, a deeper understanding of the underlying principles is crucial for anyone seeking a strong foundation in mathematics. This article will not only answer the question but also provide a comprehensive explanation, exploring different approaches and highlighting the importance of fractional understanding.
Understanding the Problem: Dividing Fractions
The core of the problem lies in understanding what we're actually doing: we're dividing one fraction (2/3) by another (1/4). This isn't about simply subtracting 1/4 repeatedly from 2/3; instead, we're asking how many times 1/4 "fits" into 2/3. This concept is fundamental to understanding division, regardless of whether the numbers are whole numbers or fractions.
Method 1: The "Keep, Change, Flip" Method (Inversion)
This popular method simplifies dividing fractions into a multiplication problem. It works by following these steps:
- Keep the first fraction the same: 2/3
- Change the division sign to a multiplication sign: ×
- Flip (or invert) the second fraction: 1/4 becomes 4/1 (or simply 4)
So, our problem becomes: (2/3) × (4/1) = 8/3
This result, 8/3, is an improper fraction. To make it easier to understand, we convert it to a mixed number:
8 ÷ 3 = 2 with a remainder of 2. Therefore, 8/3 = 2 and 2/3.
This means there are 2 and 2/3 of 1/4s in 2/3.
Method 2: Finding a Common Denominator
This method provides a more intuitive visual understanding. We begin by finding a common denominator for both fractions:
The least common multiple of 3 and 4 is 12. Therefore, we convert both fractions to have a denominator of 12:
- 2/3 = (2 × 4) / (3 × 4) = 8/12
- 1/4 = (1 × 3) / (4 × 3) = 3/12
Now, we ask: how many times does 3/12 fit into 8/12? This is equivalent to dividing 8/12 by 3/12:
(8/12) ÷ (3/12) = 8/3
As before, 8/3 simplifies to 2 and 2/3.
Method 3: Visual Representation
Imagine a pizza cut into 12 slices. 2/3 of the pizza represents 8 slices (8/12). 1/4 of the pizza represents 3 slices (3/12). How many sets of 3 slices can you make from 8 slices? You can make two complete sets (6 slices) with 2 slices remaining. This visually represents the answer: 2 and 2/3.
Why Understanding Fractions is Crucial
The seemingly simple problem of dividing 2/3 by 1/4 highlights the importance of a robust understanding of fractions. This understanding extends far beyond simple calculations and has broad applications in numerous fields, including:
- Cooking and Baking: Scaling recipes, understanding ingredient ratios.
- Construction and Engineering: Precise measurements, material calculations.
- Finance: Calculating interest, proportions, and percentages.
- Data Analysis: Interpreting proportions and percentages in datasets.
- Computer Science: Representing data and performing calculations.
Advanced Applications and Extensions
The concept of dividing fractions extends to more complex scenarios. For instance:
- Dividing fractions with larger numerators and denominators: The same principles apply, whether the numbers are simple or complex. Mastering the fundamental methods (keep, change, flip; common denominator) allows you to handle any fractional division problem.
- Dividing mixed numbers: Before dividing, convert mixed numbers into improper fractions. Then, apply the standard division methods.
- Real-world problem-solving: Many real-world problems can be modeled using fractions and require the ability to divide them.
Common Mistakes to Avoid
Several common mistakes can lead to incorrect answers when dividing fractions:
- Forgetting to invert the second fraction: This is a crucial step in the "keep, change, flip" method. Failing to invert will result in a completely wrong answer.
- Incorrectly finding the common denominator: Ensure you find the least common multiple to simplify calculations.
- Improper conversion of mixed numbers: Always convert mixed numbers to improper fractions before performing division.
- Errors in simplification: Always simplify fractions to their lowest terms to get the clearest and most accurate answer.
Practicing and Improving Your Skills
The key to mastering fraction division is practice. Here are some tips:
- Start with simple problems: Begin with easy examples to build confidence and understanding.
- Gradually increase complexity: Once you're comfortable with simple problems, move on to more complex scenarios, including mixed numbers and larger fractions.
- Use different methods: Try solving problems using multiple methods (keep, change, flip; common denominator; visual representation) to reinforce your understanding.
- Check your work: Always double-check your calculations to ensure accuracy.
- Seek help when needed: Don't hesitate to ask for assistance if you're struggling.
Conclusion: Beyond the Numbers
The question, "How many 1/4s are in 2/3?" serves as a gateway to a much deeper understanding of fractions and mathematical operations. By exploring different methods and appreciating the underlying principles, we can move beyond simple calculations and develop a stronger, more versatile mathematical foundation. This foundation is not just about solving problems; it's about cultivating critical thinking, problem-solving skills, and a deeper appreciation for the elegance and power of mathematics in our everyday lives. The answer, 2 and 2/3, is not just a numerical result; it's a testament to the beauty and precision of mathematical reasoning.
Latest Posts
Latest Posts
-
How To Calculate Wall Tile Square Footage
May 25, 2025
-
14 Is What Percent Of 21
May 25, 2025
-
How Many Days Has It Been Since August 23
May 25, 2025
-
3 Divided By 5 8 As A Fraction
May 25, 2025
-
Whats The Measure Of A Triangle
May 25, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/4 Are In 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.