3 Divided By 5/8 As A Fraction
listenit
May 25, 2025 · 5 min read
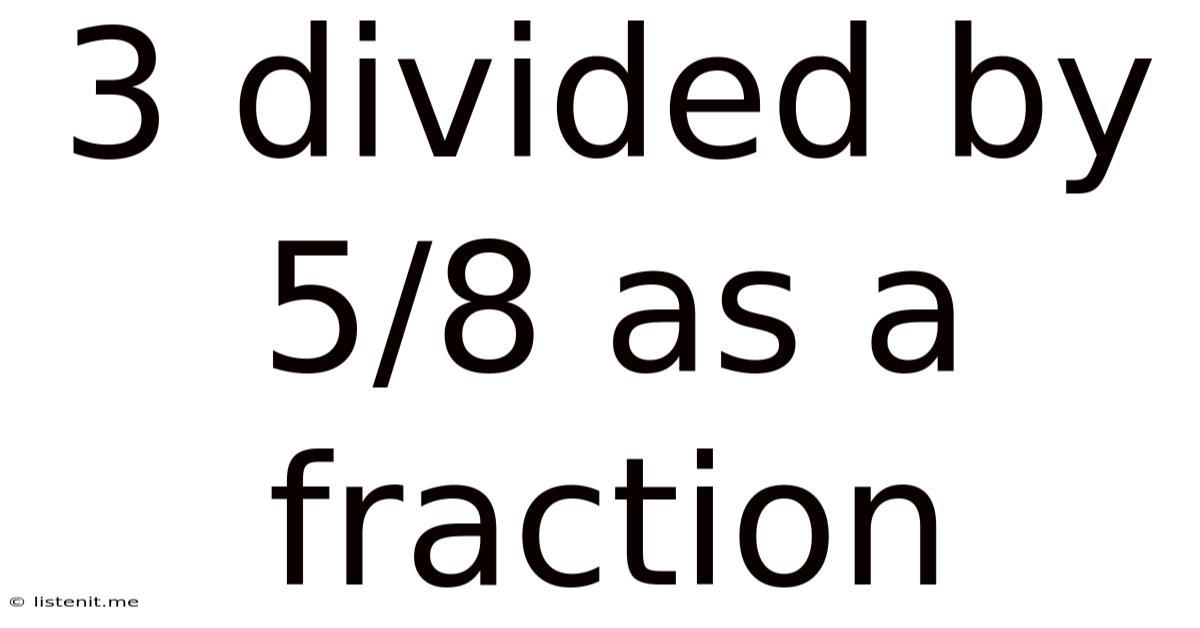
Table of Contents
3 Divided by 5/8 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through solving the problem "3 divided by 5/8 as a fraction," explaining the steps involved, providing visual aids, and offering practical applications to solidify your understanding. We'll delve into the core concepts, address common pitfalls, and explore various approaches to tackling similar problems.
Understanding the Basics: Fractions and Division
Before diving into the specific problem, let's refresh our understanding of fractions and division. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
Division, in its simplest form, is the process of splitting a quantity into equal parts. When dividing by a fraction, we're essentially asking "how many times does this fraction fit into the whole number (or another fraction)?"
Solving 3 Divided by 5/8
Now, let's tackle the problem at hand: 3 divided by 5/8. We can represent this mathematically as:
3 ÷ 5/8
To solve this, we'll use the method of inverting and multiplying. This is a fundamental technique in fraction division.
Step 1: Rewrite the Whole Number as a Fraction
First, we rewrite the whole number 3 as a fraction. Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 3 becomes 3/1.
Our problem now looks like this:
3/1 ÷ 5/8
Step 2: Invert the Second Fraction (the Divisor)
The key to dividing fractions is to invert (or "flip") the second fraction, the one we're dividing by. This means swapping the numerator and the denominator. 5/8 becomes 8/5.
Step 3: Change the Division Sign to Multiplication
Now, we change the division sign (÷) to a multiplication sign (×).
Our equation now looks like this:
3/1 × 8/5
Step 4: Multiply the Numerators and the Denominators
Now we simply multiply the numerators together and the denominators together:
(3 × 8) / (1 × 5) = 24/5
Step 5: Simplify the Result (if necessary)
In this case, the fraction 24/5 is already in its simplest form. The numerator (24) and the denominator (5) have no common factors other than 1. Therefore, our final answer is 24/5.
Visual Representation: Understanding the Result
Imagine you have 3 whole pizzas. You want to divide these pizzas into servings of 5/8 of a pizza each. How many servings will you have? The answer, 24/5, means you'll have 24 pieces, each representing 1/5 of a whole pizza. This is equivalent to 4 whole pizzas and 4/5 of a pizza.
Alternative Methods: Exploring Other Approaches
While the invert-and-multiply method is the most common and efficient, let's explore other approaches to reinforce understanding:
Method 1: Using the Reciprocal
The reciprocal of a number is simply its multiplicative inverse (1 divided by the number). The reciprocal of 5/8 is 8/5. Dividing by a fraction is the same as multiplying by its reciprocal. This approach leads us to the same solution:
3 × (8/5) = 24/5
Method 2: Long Division with Fractions
While less common, you can also perform long division using fractions. This method involves repeatedly subtracting the divisor (5/8) from the dividend (3) until you reach zero or a remainder. This approach can be more time-consuming, but it provides a different perspective on the division process. However, it is generally not recommended for this particular problem as the invert-and-multiply method is far more efficient.
Common Mistakes to Avoid
When working with fraction division, several common mistakes can lead to incorrect answers. Here are some pitfalls to watch out for:
-
Forgetting to invert the second fraction: This is the most frequent error. Remember, you must invert the fraction you are dividing by, not the fraction you are dividing into.
-
Incorrectly multiplying the fractions: Make sure to multiply the numerators together and the denominators together separately.
-
Failing to simplify the result: Always check if your final answer can be simplified by finding common factors between the numerator and denominator.
Practical Applications: Real-World Scenarios
Understanding fraction division isn't just an academic exercise; it has many real-world applications:
-
Cooking and Baking: Many recipes involve dividing ingredients into fractions, especially when scaling recipes up or down.
-
Construction and Engineering: Precise measurements and calculations in construction often involve fractions.
-
Sewing and Tailoring: Creating patterns and cutting fabric often requires dividing measurements into fractions of inches or centimeters.
-
Finance and Budgeting: Understanding fractions is crucial when working with budgets, percentages, and interest rates.
Expanding Your Knowledge: Further Exploration
To further enhance your understanding of fraction division, consider exploring these related topics:
-
Dividing mixed numbers: A mixed number contains a whole number and a fraction (e.g., 2 1/2). The process is similar to dividing fractions, but you'll need to convert the mixed numbers into improper fractions first (where the numerator is larger than the denominator).
-
Dividing decimals: Decimals can be converted into fractions, allowing you to apply the same techniques we've discussed.
-
Complex fractions: These are fractions where either the numerator or denominator (or both) contain fractions. You can simplify these by applying the same principles of fraction division.
Conclusion: Mastering Fraction Division
Mastering fraction division, including solving problems like 3 divided by 5/8, is a valuable skill with practical applications across various fields. By understanding the fundamental concepts, employing the correct method (invert and multiply), and avoiding common pitfalls, you can confidently tackle fraction division problems and expand your mathematical proficiency. Remember that consistent practice is key to solidifying your understanding and improving your speed and accuracy. Use this guide as a resource, and don't hesitate to revisit it as needed. With focused effort, you will master this crucial aspect of arithmetic.
Latest Posts
Latest Posts
-
How Fast Is 135 Km In Mph
May 25, 2025
-
How To Find Square Feet For Tile
May 25, 2025
-
How Much Aggregate Do I Need
May 25, 2025
-
How Many Calories Should A 115 Lb Woman Eat
May 25, 2025
-
8 Out Of 24 As A Percentage
May 25, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 5/8 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.