How Many 1/3 Cups Equals 2/3
listenit
Apr 05, 2025 · 6 min read
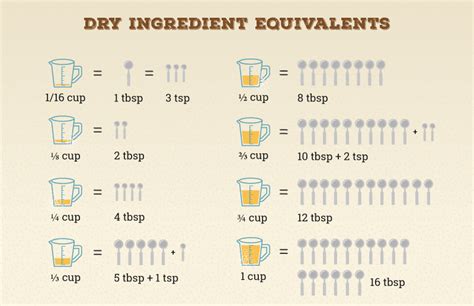
Table of Contents
How Many 1/3 Cups Equal 2/3? A Deep Dive into Fraction Conversions
Understanding fractions is fundamental to cooking, baking, and many other aspects of life. A common question that arises, especially in the kitchen, is: how many 1/3 cups equal 2/3 of a cup? This seemingly simple question opens the door to a broader understanding of fraction manipulation, a skill crucial for accurate measurements and successful recipes. This article will not only answer this question but also delve into the underlying principles of fraction equivalence, offering practical examples and exercises to solidify your understanding.
Understanding Fractions: The Basics
Before we tackle the specific question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers:
- Numerator: The top number, indicating how many parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the context of our question, we're dealing with thirds (1/3 and 2/3). The denominator, 3, tells us the whole is divided into three equal parts. The numerator indicates how many of those parts we're considering. 1/3 means one out of three equal parts, while 2/3 means two out of three equal parts.
Solving the Problem: How Many 1/3 Cups Equal 2/3 Cups?
The question "How many 1/3 cups equal 2/3 cups?" is essentially asking us to solve the equation: x * (1/3) = (2/3), where 'x' represents the number of 1/3 cups.
To solve this, we can use several methods:
Method 1: Visual Representation
Imagine a pie or a circle cut into three equal slices. 2/3 of the pie represents two of those slices. Each slice is 1/3 of the pie. Therefore, it's visually evident that two 1/3 cups equal 2/3 of a cup.
Method 2: Multiplication and Division of Fractions
This method involves multiplying both sides of the equation by the reciprocal of 1/3, which is 3/1 (or simply 3).
x * (1/3) = (2/3)
Multiply both sides by 3:
3 * x * (1/3) = 3 * (2/3)
The 3's on the left-hand side cancel each other out:
x = 3 * (2/3)
This simplifies to:
x = 6/3
Reducing the fraction:
x = 2
Therefore, two 1/3 cups equal 2/3 of a cup.
Method 3: Simple Reasoning
Since 2/3 means two parts out of three, and each part is represented by 1/3, it directly follows that two 1/3 cups will make up 2/3 of a cup. This is the most intuitive approach for this particular problem.
Extending the Concept: Working with Other Fractions
The principles used to solve the 1/3 and 2/3 problem can be applied to a wide range of fraction problems. Let's explore some examples:
Example 1: How many 1/4 cups equal 3/4 cups?
Using the same logic as above, we can determine that three 1/4 cups equal 3/4 of a cup. We can also solve this algebraically:
x * (1/4) = (3/4) x = (3/4) * (4/1) x = 12/4 x = 3
Example 2: How many 1/8 teaspoons equal 5/8 teaspoons?
Following the same pattern:
x * (1/8) = (5/8) x = (5/8) * (8/1) x = 40/8 x = 5
Five 1/8 teaspoons equal 5/8 of a teaspoon.
Example 3: Working with mixed numbers
Let's consider a slightly more complex scenario: How many 1/2 cups equal 2 1/2 cups? First, we need to convert the mixed number (2 1/2) into an improper fraction. This is done by multiplying the whole number by the denominator, adding the numerator, and keeping the same denominator.
2 1/2 = (2 * 2 + 1) / 2 = 5/2
Now we solve:
x * (1/2) = (5/2) x = (5/2) * (2/1) x = 10/2 x = 5
Therefore, five 1/2 cups equal 2 1/2 cups.
Practical Applications in Cooking and Baking
Understanding fraction conversions is critical for accurate measurements in cooking and baking. Incorrect measurements can significantly affect the outcome of a recipe. For instance:
- Following recipes: Many recipes use fractional measurements. Knowing how to convert fractions allows you to easily adjust recipes to suit your needs. If a recipe calls for 2/3 cup of sugar, and you only have a 1/3 cup measuring cup, you know exactly how many times you need to fill it.
- Scaling recipes: If you want to double or halve a recipe, you'll need to be able to accurately adjust fractional measurements. Doubling a recipe that calls for 1/3 cup of flour means you'll need 2/3 cup of flour.
- Substituting ingredients: Sometimes you might need to substitute ingredients. If you need to use a different size measuring cup or substitute ingredients in different quantities, knowledge of fraction manipulation is indispensable.
Beyond the Kitchen: Real-World Applications of Fractions
The ability to work with fractions extends far beyond the culinary arts. They are used extensively in:
- Construction and engineering: Accurate measurements and calculations are vital. Fractions are used to specify dimensions, calculate material quantities, and ensure precision in construction projects.
- Finance and accounting: Fractions are used to calculate interest rates, percentages, and proportions in financial analysis and accounting.
- Science and medicine: Fractions are used to represent ratios and proportions in scientific experiments and medical dosages.
- Data analysis: Fractions are frequently used in statistical analysis to represent proportions and probabilities within datasets.
Mastering Fractions: Tips and Practice Exercises
Mastering fractions requires consistent practice. Here are some tips to improve your understanding and skills:
- Visualize: Use diagrams, pie charts, or other visual aids to understand fractions better.
- Practice regularly: Solve various fraction problems, gradually increasing the difficulty level.
- Use different methods: Try different approaches to solve problems, such as visual representation, algebraic manipulation, or simple reasoning.
- Check your work: Always double-check your answers to ensure accuracy.
- Seek help when needed: Don't hesitate to ask for clarification or help if you're struggling with a particular concept.
Here are a few practice exercises:
- How many 1/5 cups equal 3/5 cups?
- How many 1/6 teaspoons equal 5/6 teaspoons?
- How many 1/8 cups equal 7/8 cups?
- How many 1/4 cups equal 1 1/4 cups?
- Convert 3/2 cups to a mixed number and determine how many 1/2 cups it equals.
Conclusion
Understanding how many 1/3 cups equal 2/3 cups is just the starting point. Mastering fractions is a valuable skill with wide-ranging applications. By practicing regularly and utilizing different approaches, you can confidently tackle fraction problems, improving your skills in cooking, baking, and many other aspects of your life. The ability to work comfortably with fractions unlocks a deeper understanding of numerical relationships and paves the way for success in various academic and professional endeavors. Remember that consistent practice is key to mastering this essential mathematical skill.
Latest Posts
Latest Posts
-
How Do You Write 50 As A Decimal
Apr 05, 2025
-
4 2 3 As An Improper Fraction
Apr 05, 2025
-
Complete The Square X2 6x 13
Apr 05, 2025
-
What Do Subscripts Mean In Chemistry
Apr 05, 2025
-
What Is The Lcm Of 5 And 6
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/3 Cups Equals 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
