How Do You Factor X 2 9
listenit
Apr 03, 2025 · 5 min read
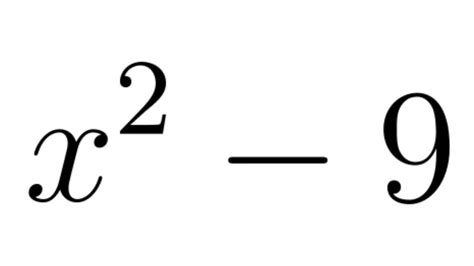
Table of Contents
How Do You Factor x² - 9? A Comprehensive Guide to Factoring Quadratic Expressions
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor these expressions opens doors to solving quadratic equations, simplifying complex algebraic expressions, and grasping more advanced mathematical concepts. This comprehensive guide will delve into the process of factoring x² - 9, explaining the underlying principles and providing various approaches to tackle similar problems. We'll cover the difference of squares method, its applications, and how to extend this knowledge to factor other quadratic expressions.
Understanding Quadratic Expressions
Before diving into the factorization of x² - 9, let's define what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and 'a' is not equal to zero.
Our specific example, x² - 9, fits this form. In this case, a = 1, b = 0, and c = -9. The absence of an 'x' term simplifies the factoring process considerably.
The Difference of Squares Method: The Key to Factoring x² - 9
The expression x² - 9 is a classic example of a difference of squares. This special type of quadratic expression is characterized by two perfect squares separated by a subtraction sign. The general form of a difference of squares is:
a² - b²
Notice that our expression, x² - 9, fits this pattern perfectly:
- a² = x² (because x * x = x²)
- b² = 9 (because 3 * 3 = 9)
The difference of squares formula provides a straightforward method for factoring this type of expression:
a² - b² = (a + b)(a - b)
Applying this formula to our expression x² - 9:
x² - 9 = (x + 3)(x - 3)
Therefore, the factored form of x² - 9 is (x + 3)(x - 3).
Verifying the Factorization
To confirm our factorization is correct, we can use the FOIL method (First, Outer, Inner, Last) to expand the factored expression:
(x + 3)(x - 3) = x² - 3x + 3x - 9 = x² - 9
As you can see, expanding the factored form returns the original expression, proving that our factorization is accurate.
Beyond x² - 9: Extending the Difference of Squares Method
The difference of squares method is not limited to simple expressions like x² - 9. It can be applied to more complex quadratic expressions, provided they follow the a² - b² pattern. Let's explore some examples:
Example 1: Factoring 4x² - 25
This expression is also a difference of squares:
- a² = 4x² (because (2x) * (2x) = 4x²)
- b² = 25 (because 5 * 5 = 25)
Applying the formula:
4x² - 25 = (2x + 5)(2x - 5)
Example 2: Factoring 16y⁴ - 81
Even higher powers can be factored using the difference of squares:
- a² = 16y⁴ (because (4y²) * (4y²) = 16y⁴)
- b² = 81 (because 9 * 9 = 81)
Applying the formula:
16y⁴ - 81 = (4y² + 9)(4y² - 9)
Notice that the second factor, 4y² - 9, is itself a difference of squares! We can further factor this expression:
4y² - 9 = (2y + 3)(2y - 3)
Therefore, the fully factored form of 16y⁴ - 81 is (4y² + 9)(2y + 3)(2y - 3).
Identifying and Applying the Difference of Squares
Successfully factoring quadratic expressions using the difference of squares method depends on correctly identifying the pattern. Here's a checklist to help you:
-
Is the expression a binomial? (meaning it has two terms) The difference of squares only applies to binomials.
-
Are both terms perfect squares? Check if each term can be expressed as the square of another expression. Remember that perfect squares are numbers or expressions that result from squaring a number or expression (e.g., 9, 16x², 25y⁴, etc.).
-
Is there a subtraction sign between the terms? The difference of squares applies only when there's a subtraction operation. Expressions like a² + b² cannot be factored using this method.
If all three conditions are met, you can confidently apply the difference of squares formula: a² - b² = (a + b)(a - b).
Solving Quadratic Equations Using Factoring
Factoring quadratic expressions is crucial for solving quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0. If you can factor the quadratic expression, you can find the values of x that make the equation true. This is because the zero product property states that if the product of two factors is zero, then at least one of the factors must be zero.
Example: Solve the equation x² - 9 = 0
We've already factored x² - 9 as (x + 3)(x - 3). Setting the equation equal to zero, we get:
(x + 3)(x - 3) = 0
By the zero product property, either (x + 3) = 0 or (x - 3) = 0. Solving these individual equations gives us the solutions:
x = -3 or x = 3
Common Mistakes to Avoid
While factoring using the difference of squares method is relatively straightforward, some common mistakes can occur:
- Incorrect identification of perfect squares: Ensure you accurately identify the 'a' and 'b' terms as perfect squares before applying the formula.
- Forgetting the subtraction sign: The method only works for differences, not sums, of squares.
- Incomplete factoring: Always check if the resulting factors can be factored further.
Conclusion: Mastering the Art of Factoring
Factoring quadratic expressions, particularly those that conform to the difference of squares pattern, is a critical algebraic skill. Understanding the underlying principles and mastering the techniques described in this guide will significantly improve your ability to solve quadratic equations, simplify complex expressions, and progress to more advanced mathematical topics. Remember to practice regularly and carefully review the steps involved to build confidence and accuracy in your factoring skills. By consistently applying these methods and being mindful of common errors, you'll become proficient in factoring quadratic expressions and unlock a deeper understanding of algebra.
Latest Posts
Latest Posts
-
What Organelle Is Missing From The Red Blood Cells
Apr 04, 2025
-
1s2 2s2 2p5 Ion With 1 Charge
Apr 04, 2025
-
The Arrow In A Chemical Equation Means
Apr 04, 2025
-
96 Ounces Equals How Many Pounds
Apr 04, 2025
-
5x 2y 10 In Slope Intercept Form
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How Do You Factor X 2 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
