How Are A Parallelogram And Rhombus Different
listenit
Mar 28, 2025 · 5 min read
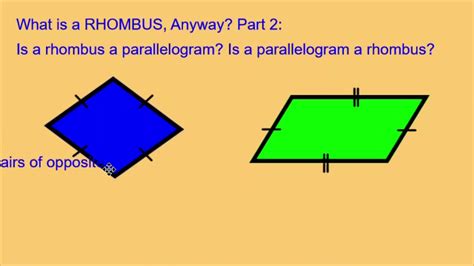
Table of Contents
How Are a Parallelogram and Rhombus Different? A Comprehensive Guide
Understanding the nuances between geometric shapes can be tricky, especially when dealing with quadrilaterals like parallelograms and rhombuses. While they share some similarities, key differences set them apart. This comprehensive guide will delve into the distinct characteristics of parallelograms and rhombuses, helping you grasp their unique properties and identify them with confidence. We'll explore their definitions, properties, formulas, and even touch upon real-world applications.
Defining Parallelograms and Rhombuses
Before diving into their differences, let's solidify our understanding of each shape individually.
What is a Parallelogram?
A parallelogram is a quadrilateral (a four-sided polygon) where opposite sides are parallel and equal in length. This fundamental characteristic leads to several other properties, as we will see. Think of it as a pushed-over rectangle – it's still a four-sided figure with opposite sides parallel, but the angles aren't necessarily right angles.
What is a Rhombus?
A rhombus, often referred to as a diamond, is a special type of parallelogram. The key distinction is that a rhombus has all four sides equal in length. While this immediately sets it apart from a general parallelogram, it still retains the parallel opposite sides characteristic inherited from its parent shape, the parallelogram.
Key Differences: A Comparative Analysis
Now, let's highlight the crucial differences between parallelograms and rhombuses. These distinctions arise from the unique constraints imposed on their side lengths and angles.
| Feature | Parallelogram | Rhombus |
|---|---|---|
| Side Lengths | Opposite sides are equal; adjacent sides may differ | All four sides are equal |
| Angles | Opposite angles are equal; adjacent angles are supplementary (add up to 180°) | Opposite angles are equal; adjacent angles are supplementary |
| Diagonals | Diagonals bisect each other | Diagonals bisect each other and are perpendicular |
| Symmetry | Has rotational symmetry of order 2 | Has rotational symmetry of order 2 and two lines of reflectional symmetry |
1. Side Lengths: The Fundamental Distinction
This is the most straightforward difference. A parallelogram only requires opposite sides to be equal. Imagine a rectangle that's been skewed; it's still a parallelogram, but its adjacent sides are clearly of different lengths. A rhombus, however, demands that all four sides are congruent (equal in length). This constraint significantly impacts its other properties.
2. Diagonals: A Telling Difference
Both parallelograms and rhombuses have diagonals that bisect (cut each other in half). However, the rhombus boasts an additional property: its diagonals are perpendicular to each other. This means they intersect at a 90-degree angle. This perpendicularity is a direct consequence of the equal side lengths. In a parallelogram, the diagonals are generally not perpendicular, unless it happens to also be a rectangle (a special case).
3. Angles: Supplementary but Different
While both shapes have opposite angles that are equal and adjacent angles that are supplementary (add up to 180°), the equal side lengths of the rhombus enforce a stronger condition on its angles. In a parallelogram, the angles can be of any size as long as the opposite angles are equal and adjacent angles are supplementary. A rhombus, however, possesses more symmetry due to its equal sides.
4. Symmetry: A Visual Representation of Differences
Symmetry is a powerful tool for visually distinguishing between parallelograms and rhombuses. A parallelogram has rotational symmetry of order 2 (it looks the same after a 180° rotation). A rhombus, however, has both rotational symmetry of order 2 and two lines of reflectional symmetry. These lines of symmetry pass through opposite vertices and bisect the opposite angles.
Real-World Applications: Seeing Shapes in Action
Understanding the differences between parallelograms and rhombuses extends beyond theoretical geometry; these shapes appear frequently in the real world:
-
Parallelograms: You'll find parallelogram-shaped structures in architecture, such as the sides of some buildings or certain window designs. They're also frequently found in engineering and design, particularly in frameworks and load-bearing structures. Think of the rungs of a ladder which can be modeled as parallelograms.
-
Rhombuses: The classic example is a diamond. Rhombus shapes are prevalent in various designs, from jewelry and logos to tiles and paving stones. The inherent symmetry of the rhombus makes it aesthetically pleasing and structurally sound in many applications. Also consider the way certain crystals form—their structures often exhibit rhombic symmetry.
Formulas and Calculations: A Deeper Dive
While both shapes share some common formulas (like area calculations involving base and height), the rhombus has some unique formulas due to its equal sides and perpendicular diagonals.
Parallelogram Formulas:
- Area: Base × Height
- Perimeter: 2 × (a + b) (where 'a' and 'b' are the lengths of adjacent sides)
Rhombus Formulas:
- Area: Base × Height OR (1/2) × d1 × d2 (where d1 and d2 are the lengths of the diagonals)
- Perimeter: 4 × s (where 's' is the length of one side, since all sides are equal)
Understanding these formulas allows you to calculate the area and perimeter of these shapes efficiently. Remember to correctly identify the shape before applying the relevant formulas.
Advanced Concepts and Related Shapes
The study of parallelograms and rhombuses can lead to exploring more complex geometric concepts and related shapes.
Special Cases: Rectangles and Squares
- Rectangle: A rectangle is a special type of parallelogram where all angles are right angles (90°).
- Square: A square is a special type of rhombus (and rectangle) where all angles are right angles and all sides are equal.
The square embodies the properties of both a parallelogram and a rhombus, showcasing the hierarchical relationship between these shapes.
Conclusion: Recognizing the Distinctions
By understanding the fundamental differences in side lengths, angles, diagonals, and symmetry, you can confidently differentiate between parallelograms and rhombuses. This knowledge is valuable not just in geometry but also in various fields where these shapes play a significant role. Remember the core distinction: all sides equal defines a rhombus; just opposite sides equal defines a parallelogram. With this understanding, you can approach geometric problems with greater clarity and precision. Furthermore, exploring the real-world applications of these shapes strengthens your understanding and highlights their importance in everyday life.
Latest Posts
Latest Posts
-
How Do You Find The Mass Of A Cube
Mar 31, 2025
-
What Color Of Light Has The Highest Energy
Mar 31, 2025
-
Balanced Equation Of Magnesium And Hydrochloric Acid
Mar 31, 2025
-
Lowest Common Multiple Of 25 And 30
Mar 31, 2025
-
Whats The Square Root Of 576
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Are A Parallelogram And Rhombus Different . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
