Graph X 3 On A Number Line
listenit
Mar 30, 2025 · 6 min read
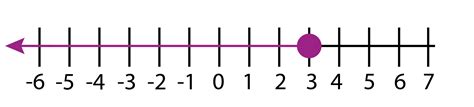
Table of Contents
Graphing x = 3 on a Number Line: A Comprehensive Guide
Graphing equations on a number line might seem simple, especially when dealing with a straightforward equation like x = 3. However, understanding the underlying concepts and their implications is crucial for building a strong foundation in algebra and beyond. This comprehensive guide will explore graphing x = 3 on a number line, delve into the intricacies of the equation, and explain its significance in various mathematical contexts.
Understanding the Equation x = 3
The equation x = 3 is a linear equation in one variable. It signifies that the variable 'x' has only one possible value: 3. This differs from equations like y = 2x + 1, where 'y' depends on the value of 'x' and represents a line on a coordinate plane (requiring two axes). In contrast, x = 3 represents a single point on a number line.
Graphing x = 3 on a Number Line: A Step-by-Step Approach
A number line is a visual representation of numbers, typically arranged from least to greatest, extending infinitely in both positive and negative directions. Graphing x = 3 on a number line involves identifying the position of the number 3 on the line and marking it appropriately.
Step 1: Draw a Number Line
Begin by drawing a straight horizontal line. This line represents the number line itself.
Step 2: Mark Key Points
Mark some key points on your number line, including zero (0) as the center point and a few positive and negative integers for context. For example, mark -3, -2, -1, 0, 1, 2, 3, 4, 5. This gives a clear scale and helps visualize the position of 3.
Step 3: Locate and Mark x = 3
Locate the point representing the number 3 on the number line. This point will usually be towards the right of zero. Now, mark this point using a solid dot (•) or a small vertical line. This precise point represents the solution to the equation x = 3.
Step 4: Label the Point
Label the marked point as "x = 3" to clearly indicate that this point corresponds to the solution of the given equation. This crucial step improves clarity and understanding, particularly when dealing with multiple equations or points on a single number line.
Interpreting the Graph of x = 3
The graph of x = 3 on a number line shows a single point. This simplicity underscores a critical concept: the equation dictates that 'x' can only be equal to 3; no other value satisfies the equation. This contrasts with equations that might have multiple solutions or an infinite number of solutions.
Expanding the Concept: Types of Equations and their Graphical Representations on a Number Line
While x = 3 represents a specific instance, it's valuable to understand how different equations appear on a number line:
1. Inequalities on a Number Line:
Inequalities like x > 3 (x is greater than 3), x < 3 (x is less than 3), x ≥ 3 (x is greater than or equal to 3), and x ≤ 3 (x is less than or equal to 3) are represented by intervals on the number line.
- x > 3: An open circle (◦) is placed at 3, and an arrow extends to the right, indicating all values greater than 3.
- x < 3: An open circle (◦) is placed at 3, and an arrow extends to the left, indicating all values less than 3.
- x ≥ 3: A closed circle (•) is placed at 3, and an arrow extends to the right, including 3 and all values greater than 3.
- x ≤ 3: A closed circle (•) is placed at 3, and an arrow extends to the left, including 3 and all values less than 3.
2. Compound Inequalities on a Number Line:
Compound inequalities, such as 2 < x < 5 (x is greater than 2 and less than 5), combine two inequalities. These are represented by an interval between two points on the number line. In this case, open circles would be at 2 and 5, and a line would connect them, representing all values between 2 and 5 (excluding 2 and 5 themselves).
3. Equations with Multiple Solutions on a Number Line:
Equations with multiple solutions, like x² = 4 (which has solutions x = 2 and x = -2), are represented by multiple points on the number line. Each solution would be marked with a solid dot.
The Significance of x = 3 in Various Mathematical Contexts
While seemingly basic, the equation x = 3, and its graphical representation, finds applications in many areas of mathematics:
1. Solving Equations:
It forms the foundation of solving more complex equations. Understanding the solution x = 3 allows for a grasp of more intricate algebraic procedures.
2. Coordinate Geometry:
In coordinate geometry, the line x = 3 is a vertical line passing through the point (3, y) for any value of y. This is a fundamental concept in understanding lines and their equations.
3. Set Theory:
The solution x = 3 can be viewed as a singleton set {3}, containing only one element. This relates to concepts in set theory and their visual representations.
4. Linear Algebra:
The concept extends to linear algebra, particularly in dealing with systems of equations, where understanding simple equations like x = 3 lays the groundwork for solving more complex systems.
5. Calculus:
Although not directly used in the core calculations, understanding the representation of a single point on a number line is crucial for grasping concepts in calculus involving limits and derivatives.
Practical Applications and Real-World Examples
While the equation x = 3 might seem abstract, its principles have practical applications:
- Measuring: If 'x' represents the length of a certain object, and the measurement is 3 units (e.g., 3 meters, 3 centimeters), then x = 3 reflects this precise measurement.
- Counting: If x represents the number of items, and you have exactly 3 items, then x = 3 accurately represents the count.
- Data Representation: In simple data sets, if a single variable holds a constant value of 3, then x = 3 is used to depict that value.
- Programming: In computer programming, assigning a value of 3 to a variable is represented using a similar assignment statement, like
x = 3.
Troubleshooting Common Mistakes
While seemingly straightforward, some common errors can occur when graphing x = 3:
- Confusing the number line with a coordinate plane: Remember, x = 3 is represented on a single number line, not a coordinate plane (which uses two axes, x and y).
- Incorrectly marking the point: Ensure you mark the point precisely at 3 and not slightly to the left or right.
- Failing to label the point: Always label the marked point as "x = 3" for clarity.
- Misunderstanding the meaning of the equation: Remember that x = 3 means that the only value of x that satisfies the equation is 3.
Conclusion: Mastering the Basics for Future Success
Graphing x = 3 on a number line, although seemingly a simple task, underpins many critical concepts in mathematics. By understanding the equation's meaning, the steps involved in graphing it, and its broader mathematical implications, you build a solid foundation for more advanced mathematical concepts. The ability to accurately represent equations on a number line serves as a fundamental skill that enhances your comprehension of various mathematical ideas and contributes to a stronger grasp of algebra and beyond. Consistent practice and attention to detail will solidify your understanding and help you avoid common mistakes, setting the stage for success in more complex mathematical endeavors.
Latest Posts
Latest Posts
-
Solve This Equation 4y 228 352
Apr 01, 2025
-
Oxidation Reactions Are Coupled With Reactions
Apr 01, 2025
-
Whats Half Of 1 And 1 2
Apr 01, 2025
-
Why Is Water Liquid At Room Temperature
Apr 01, 2025
-
How To Determine The Density Of A Solid
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Graph X 3 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
