Graph X 2 X 2 9
listenit
Apr 07, 2025 · 5 min read
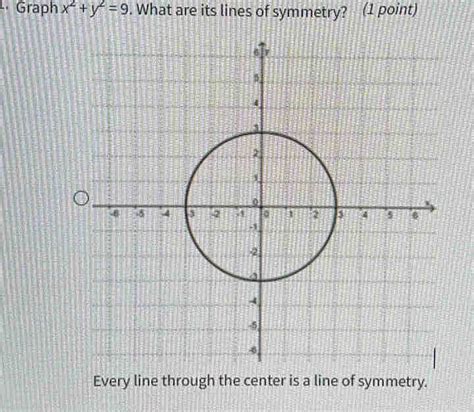
Table of Contents
Exploring the Graph of x² + 2x + 9: A Deep Dive into Quadratic Functions
The seemingly simple equation, x² + 2x + 9, hides a wealth of mathematical properties waiting to be explored. This article will delve into a comprehensive analysis of this quadratic function, examining its graph, key features, and the broader implications within the field of mathematics. We'll move beyond simply plotting points and uncover the deeper understanding necessary for truly grasping its behavior.
Understanding Quadratic Functions: A Foundation
Before embarking on a detailed analysis of x² + 2x + 9, let's establish a solid understanding of quadratic functions in general. A quadratic function is a polynomial function of degree two, meaning the highest power of the variable (x in this case) is 2. They are generally represented in the form:
f(x) = ax² + bx + c
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (otherwise, it wouldn't be a quadratic). This standard form allows us to quickly identify key features of the parabola, the distinctive U-shaped curve that represents a quadratic function.
Key Features of a Parabola
Several characteristics define a parabola and its behavior:
- Vertex: The turning point of the parabola, representing either the minimum (if 'a' > 0) or maximum (if 'a' < 0) value of the function.
- Axis of Symmetry: A vertical line that passes through the vertex, dividing the parabola into two symmetrical halves.
- x-intercepts (Roots or Zeros): The points where the parabola intersects the x-axis (where y = 0). These represent the solutions to the quadratic equation f(x) = 0.
- y-intercept: The point where the parabola intersects the y-axis (where x = 0). This is simply the value of 'c' in the standard form.
- Concavity: Describes whether the parabola opens upwards (concave up, if 'a' > 0) or downwards (concave down, if 'a' < 0).
Analyzing x² + 2x + 9: A Step-by-Step Approach
Now, let's apply this knowledge to our specific equation: x² + 2x + 9. Here, a = 1, b = 2, and c = 9.
1. Determining the Concavity
Since 'a' = 1 (positive), the parabola opens upwards, meaning it has a minimum value.
2. Finding the Vertex
The x-coordinate of the vertex can be found using the formula:
x = -b / 2a
In our case: x = -2 / (2 * 1) = -1
To find the y-coordinate, substitute this x-value back into the original equation:
y = (-1)² + 2(-1) + 9 = 8
Therefore, the vertex of the parabola is (-1, 8).
3. Identifying the Axis of Symmetry
The axis of symmetry is a vertical line passing through the vertex. Its equation is simply:
x = -1
4. Calculating the y-intercept
The y-intercept is the value of the function when x = 0. From the equation, we can directly see that the y-intercept is (0, 9).
5. Finding the x-intercepts (Roots)
The x-intercepts are found by setting f(x) = 0 and solving the quadratic equation:
x² + 2x + 9 = 0
We can use the quadratic formula to solve for x:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values:
x = [-2 ± √(2² - 4 * 1 * 9)] / (2 * 1) = [-2 ± √(-32)] / 2
Notice that the discriminant (b² - 4ac = -32) is negative. This indicates that there are no real x-intercepts. The parabola does not intersect the x-axis. The roots are complex numbers.
6. Sketching the Graph
With all this information, we can now sketch the graph of x² + 2x + 9. It's an upward-opening parabola with a vertex at (-1, 8), an axis of symmetry at x = -1, a y-intercept at (0, 9), and no x-intercepts.
Further Exploration and Applications
The analysis above provides a foundational understanding of the graph of x² + 2x + 9. However, we can delve deeper into its properties and applications:
1. Complex Roots and the Complex Plane
The fact that the quadratic equation has no real roots doesn't mean it has no solutions. The solutions are complex numbers, involving the imaginary unit 'i' (where i² = -1). These complex roots can be visualized on the complex plane, providing a richer understanding of the equation's complete solution set.
2. Transformations of Quadratic Functions
Understanding the relationship between the standard form of a quadratic function (ax² + bx + c) and its graph allows for the prediction of how changes in 'a', 'b', and 'c' will affect the parabola's position, shape, and orientation. This concept of transformations is fundamental in understanding the broader family of quadratic functions.
3. Applications in Physics and Engineering
Quadratic functions have numerous real-world applications, especially in fields like physics and engineering. For example, they describe projectile motion under the influence of gravity, the shape of a parabolic antenna, or the trajectory of a ball thrown in the air. The understanding of the vertex, intercepts and other properties becomes crucial in these applications.
4. Calculus and Optimization
In calculus, quadratic functions are used to model optimization problems. Finding the vertex of a parabola is equivalent to finding the maximum or minimum value of the function, which has significant implications in various fields.
Conclusion: Beyond the Surface
The seemingly simple equation x² + 2x + 9 presents a rich opportunity for exploring the fascinating world of quadratic functions. By understanding its key features, including its vertex, axis of symmetry, intercepts (both real and complex), and concavity, we gain a deeper appreciation of its mathematical properties and its numerous applications across diverse fields. This detailed analysis serves as a springboard for further investigation into the broader landscape of polynomial functions and their significance in mathematics and beyond. Remember, the beauty of mathematics lies not just in the solutions, but in the journey of understanding how we arrive at them. The exploration of x² + 2x + 9 provides a perfect example of this enriching intellectual pursuit.
Latest Posts
Latest Posts
-
What Biomolecule Are Enzymes Made Of
Apr 08, 2025
-
3 Is 40 Percent Of What
Apr 08, 2025
-
How Many Units In A Milligram
Apr 08, 2025
-
Graph Of Absolute Value Of X 1
Apr 08, 2025
-
What Are The Steps Of The Dna Ladder Made Of
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Graph X 2 X 2 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.